What Is 1/2 To The Power Of 3
News Co
Apr 13, 2025 · 5 min read
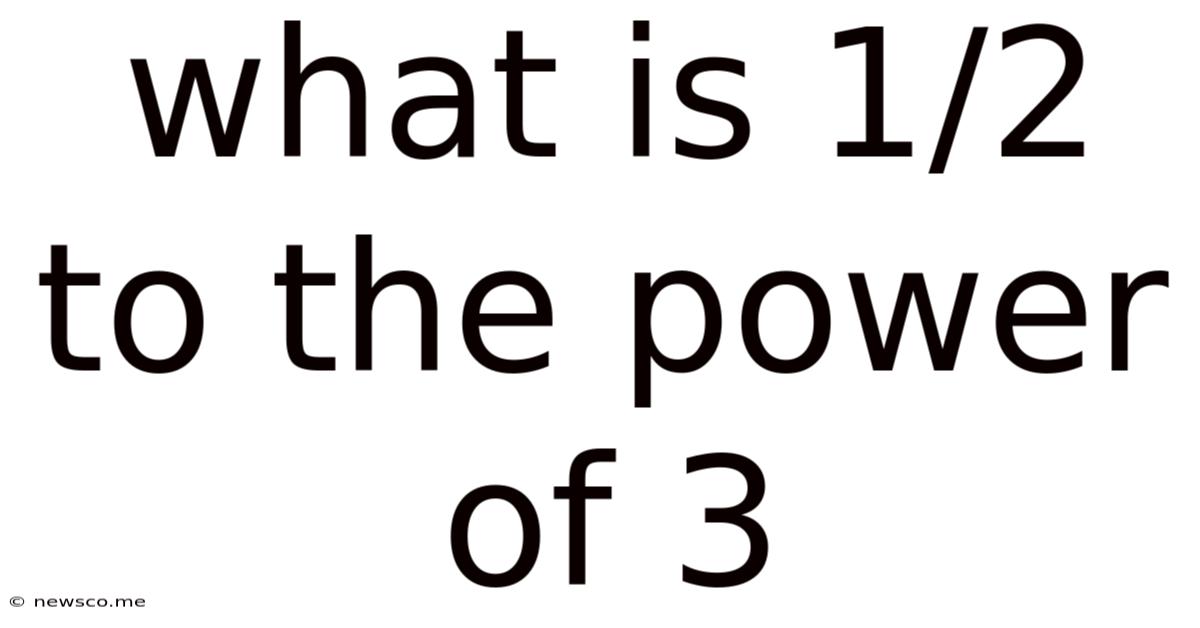
Table of Contents
What is 1/2 to the Power of 3? A Deep Dive into Exponents and Fractions
Understanding exponents and fractions is fundamental to mathematics, and mastering their interplay is crucial for various fields, from basic arithmetic to advanced calculus. This article explores the seemingly simple question, "What is 1/2 to the power of 3?" But instead of just providing the answer, we'll delve into the underlying principles, providing a comprehensive understanding of exponents, fractions, and their combined operation. We'll explore practical applications and tackle related concepts, making this a valuable resource for anyone looking to solidify their understanding of these mathematical building blocks.
Understanding Exponents
Before tackling the specific problem, let's establish a firm grasp of exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. It's written as a superscript number to the right of the base. For example:
- 2³ means 2 × 2 × 2 = 8. Here, 2 is the base, and 3 is the exponent.
- 5² means 5 × 5 = 25. Here, 5 is the base, and 2 is the exponent.
- x⁴ means x × x × x × x. Here, x is the base, and 4 is the exponent.
The exponent dictates the number of times the base is used as a factor in the multiplication. This seemingly simple concept forms the basis for numerous advanced mathematical operations.
Understanding Fractions
Fractions represent parts of a whole. They are expressed as a ratio of two integers, the numerator (top number) and the denominator (bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator indicates the number of parts considered. For example:
- 1/2 represents one-half, meaning one out of two equal parts.
- 3/4 represents three-quarters, meaning three out of four equal parts.
- 5/8 represents five-eighths, meaning five out of eight equal parts.
Fractions can be simplified by dividing both the numerator and the denominator by their greatest common divisor (GCD). For instance, 6/8 can be simplified to 3/4 by dividing both by 2.
Combining Exponents and Fractions: (1/2)³
Now, let's combine our understanding of exponents and fractions to solve the problem: (1/2)³. This means we need to multiply the fraction (1/2) by itself three times:
(1/2)³ = (1/2) × (1/2) × (1/2)
To multiply fractions, we multiply the numerators together and the denominators together:
(1 × 1 × 1) / (2 × 2 × 2) = 1/8
Therefore, (1/2)³ = 1/8.
Further Exploration: Negative Exponents and Fractional Exponents
Our exploration doesn't end here. Let's delve into more advanced scenarios involving exponents and fractions.
Negative Exponents
A negative exponent indicates the reciprocal of the base raised to the positive power of that exponent. For example:
- 2⁻² = 1/2² = 1/4
- (1/3)⁻¹ = 1/(1/3) = 3
- x⁻ⁿ = 1/xⁿ
Essentially, a negative exponent "flips" the fraction.
Fractional Exponents
Fractional exponents introduce the concept of roots. A fractional exponent a/b means taking the b-th root of the base raised to the power of a. For example:
- 4^(1/2) = √4 = 2 (The square root of 4)
- 8^(1/3) = ³√8 = 2 (The cube root of 8)
- x^(a/b) = (b√x)ᵃ
Fractional exponents elegantly connect exponents and roots, providing a unified framework for working with both.
Real-World Applications
The concept of raising fractions to powers has numerous practical applications across various fields:
-
Compound Interest: Calculating compound interest involves raising fractions to powers. For example, if you invest money with an interest rate expressed as a fraction, you'll need to raise that fraction to a power to determine the final amount after a certain number of periods.
-
Probability: In probability theory, calculating the likelihood of multiple independent events occurring involves multiplying probabilities, which are often represented as fractions. Raising a probability (a fraction) to a power helps determine the probability of that event occurring repeatedly.
-
Decay Processes: In fields like physics and chemistry, exponential decay processes are modeled using equations that involve raising fractions (representing decay rates) to powers to predict the remaining quantity after a certain time.
-
Geometry and Scaling: Scaling objects in geometry often involves multiplying dimensions by a factor, which could be represented as a fraction. Raising that fraction to a power might be necessary when dealing with volume or area scaling.
Further Practice Problems
To solidify your understanding, try solving these problems:
- (1/3)²
- (2/5)³
- (3/4)⁻²
- (16)^(1/4)
- (27)^(2/3)
These exercises will help reinforce your understanding of exponents and fractions and their interaction. Remember to follow the rules of multiplication for fractions and the interpretations of negative and fractional exponents.
Conclusion
While the initial question, "What is 1/2 to the power of 3?" seems straightforward, it opens the door to a deeper understanding of exponents and fractions and their combined operation. Mastering these concepts is crucial for success in mathematics and its various applications in science, engineering, finance, and other fields. By understanding the principles outlined in this article, you'll be well-equipped to tackle more complex problems and appreciate the elegance and power of mathematical operations. Remember to practice consistently to solidify your understanding and build confidence in tackling mathematical challenges. The more you practice, the easier and more intuitive these concepts will become. Embrace the challenge, and enjoy the journey of mathematical discovery!
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 1/2 To The Power Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.