What Is 1 3 1 3 Equal
News Co
Apr 17, 2025 · 6 min read
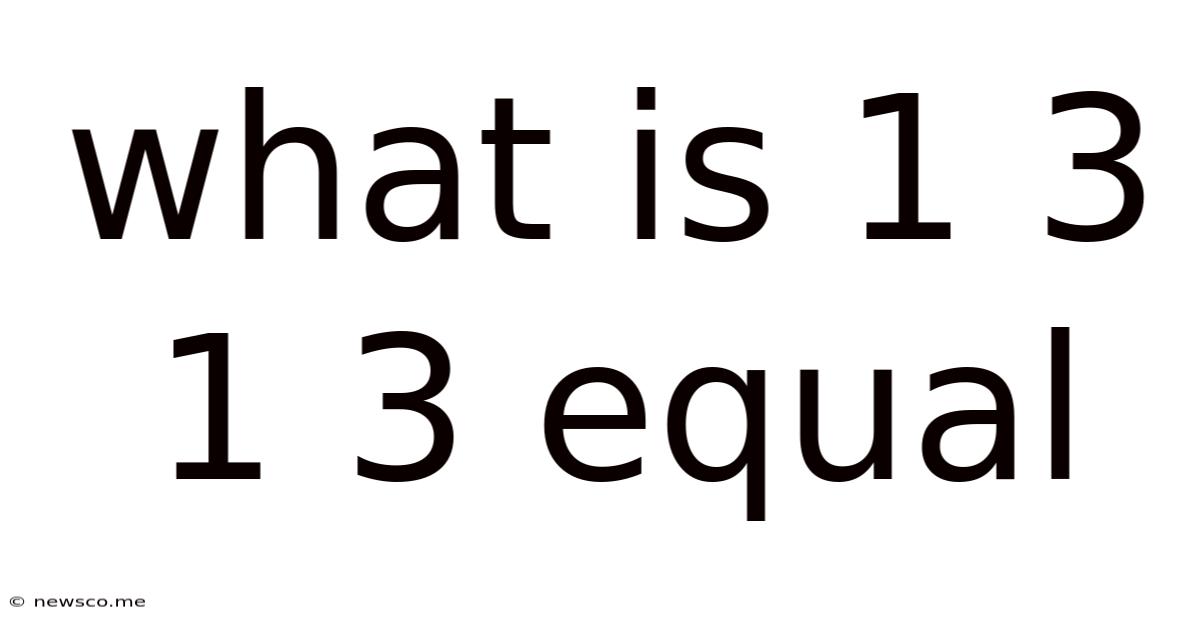
Table of Contents
What is 1 3 1 3 Equal? Unraveling the Mystery Behind Number Sequences
The seemingly simple question, "What is 1 3 1 3 equal?" might seem trivial at first glance. However, depending on the context, this sequence of numbers can represent a variety of things, from a simple addition problem to a more complex mathematical sequence or even a code. This article dives deep into the various possibilities, exploring the mathematical interpretations, potential real-world applications, and the importance of understanding context in interpreting numerical data.
1. The Obvious: Simple Addition
The most straightforward answer is that 1 + 3 + 1 + 3 = 8. This is the immediate solution if we interpret the sequence as a simple addition problem. While simplistic, this approach highlights the importance of clarifying the operation intended when presented with a numerical sequence. Context is key, and without further information, this remains the most likely and logical interpretation.
2. Exploring Mathematical Sequences and Patterns
Beyond simple addition, the sequence 1 3 1 3 could represent a more intricate mathematical pattern or sequence. Let's explore some possibilities:
2.1. Repeating Sequence: The sequence could be a repeating pattern, suggesting a continuation of 1 3 1 3 1 3… This pattern doesn't inherently have a single "equal" value, but rather defines a repetitive sequence. The value depends on how many repetitions are considered.
2.2. Fibonacci-like Sequence (with Modification): While not a direct Fibonacci sequence (where each number is the sum of the two preceding ones), it shares a similar structure of repeated elements. One could imagine a modified Fibonacci-like sequence built around this pattern, although more terms would be needed to establish a concrete definition and a clear mathematical rule for generating subsequent numbers.
2.3. Alternating Sequence: The sequence shows an alternating pattern of 1 and 3. This could be part of a larger alternating sequence with different numbers. Again, without further terms or a defined rule, determining a definitive "equal" value is impossible.
3. Delving into the World of Codes and Cryptography
In the realm of coding and cryptography, numerical sequences often represent something beyond their face value. The sequence 1 3 1 3 might represent:
3.1. A Simple Substitution Cipher: Each number could represent a letter in an alphabet. For instance, if 1 = A and 3 = C, then 1 3 1 3 could translate to "ACA." However, the limitations of a limited set of numbers are apparent; a more robust code would need a larger numerical set or use of other symbols.
3.2. Part of a More Complex Code: The sequence could be a fragment of a larger, more complex code. It might serve as a key, an identifier, or a part of a more intricate encryption algorithm. The meaning would be entirely dependent on the full code's structure and decryption key.
3.3. Binary or other Numerical Systems: If we consider other numerical systems, the interpretation can significantly change. For instance, in binary (a base-2 system), 1 and 3 wouldn't have a direct translation, requiring conversion to a base-10 representation first. Similarly, other number systems like hexadecimal (base-16) could also lead to various interpretations depending on how the sequence is translated.
4. Real-world Applications: Where Might We Encounter This Sequence?
Though seemingly simple, the 1 3 1 3 sequence, or variations of it, might occur in various real-world contexts:
4.1. Data Representation: In databases or spreadsheets, the sequence could represent any data. For example, it might represent product IDs, customer IDs, or any arbitrary data field. The meaning would depend entirely on the database schema and context.
4.2. Signal Processing: In signal processing, such a sequence could represent a simplified signal, although more complex signals would typically involve a larger range of numbers and a more structured pattern. Analyzing the sequence in signal processing would rely on additional information about its source and method of generation.
4.3. Inventory or Stock Management: The numbers could represent stock levels, quantities, or even represent simple codes for different items in a warehouse or store. The precise meaning would be defined by the inventory system's internal coding structure.
5. The Importance of Context and Further Information
The ambiguity surrounding the meaning of "1 3 1 3" underscores the critical importance of context in interpreting numerical data. Without additional information, definitive conclusions cannot be drawn. To properly interpret this sequence, we would need to know:
- The intended operation: Is it addition, multiplication, a code, or something else entirely?
- The broader context: Where did this sequence originate? What system or process generated it?
- The numerical system: Is it base-10, binary, hexadecimal, or another numerical system?
- The presence of additional data: Are there other numbers or symbols associated with this sequence?
By considering these questions, the seemingly simple question becomes a fascinating exploration into the multiple potential meanings hidden within a short sequence of numbers. This highlights the importance of critical thinking and the need for complete information when analyzing any data, even what appears to be a simple numerical pattern.
6. Expanding the Scope: Similar Numerical Sequences and their Interpretations
Exploring similar sequences can further illuminate the concept of contextual interpretation. Imagine slightly modified sequences such as:
- 1, 2, 3, 4: This is a simple arithmetic progression.
- 1, 4, 9, 16: This represents perfect squares (1², 2², 3², 4²).
- 1, 1, 2, 3, 5, 8: This is the beginning of the Fibonacci sequence.
Each of these sequences has a clear mathematical definition and interpretation. In contrast, the 1 3 1 3 sequence’s ambiguity highlights the importance of clarifying assumptions and seeking additional information when encountering a numerical sequence without a clear context.
7. Conclusion: The Power of Context in Data Analysis
The question, "What is 1 3 1 3 equal?" demonstrates the crucial role context plays in interpreting numerical data. While simple addition provides the most straightforward answer (8), the possibilities extend far beyond basic arithmetic. From potential mathematical sequences and codes to real-world applications, the correct interpretation depends heavily on the context in which the sequence appears. This exploration underscores the need for critical thinking, thorough investigation, and the recognition that seemingly simple data can hold complex and multifaceted meanings. The mystery of 1 3 1 3 is not about finding a single answer, but rather understanding the diverse possibilities inherent in incomplete data. The ability to correctly interpret such sequences is crucial in various fields, from cryptography and data analysis to signal processing and inventory management. Understanding context is the key to unlocking the true meaning of any numerical sequence.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 1 3 1 3 Equal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.