What Is 1 3/4 Divided By 2 As A Fraction
News Co
May 08, 2025 · 4 min read
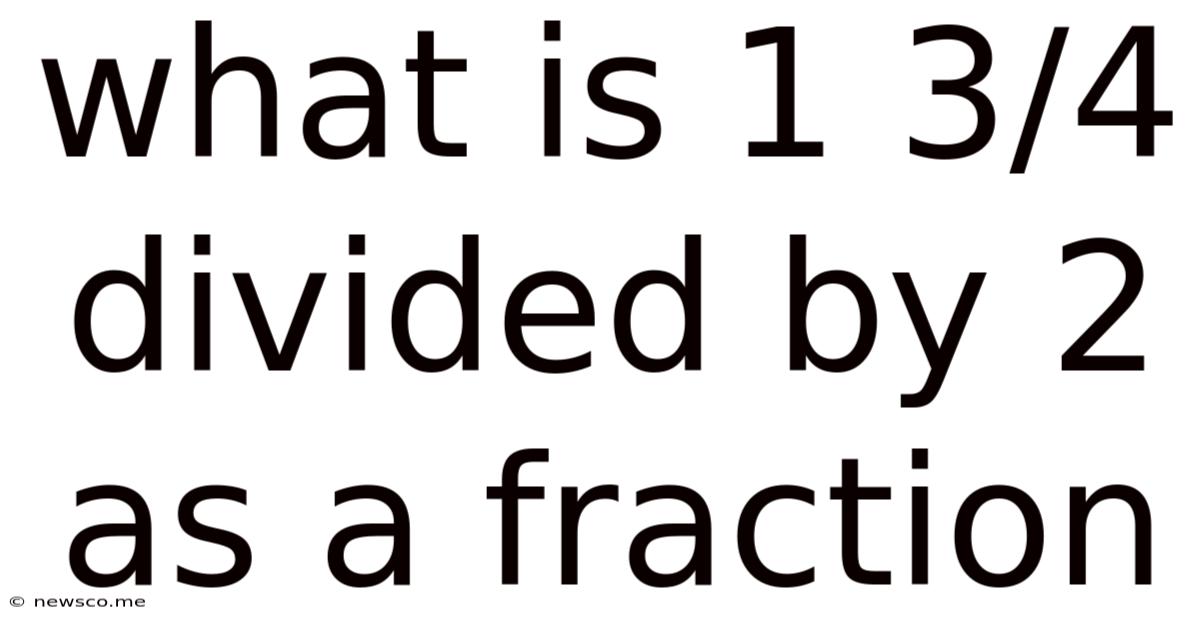
Table of Contents
What is 1 3/4 Divided by 2 as a Fraction? A Comprehensive Guide
Dividing fractions can seem daunting, especially when mixed numbers are involved. But fear not! This comprehensive guide will walk you through the process of solving 1 3/4 divided by 2, explaining the steps clearly and providing additional examples to solidify your understanding. We’ll also explore the underlying mathematical principles and offer tips for tackling similar problems with confidence.
Understanding the Problem: 1 3/4 ÷ 2
The problem, "What is 1 3/4 divided by 2 as a fraction?", asks us to perform a division operation involving a mixed number (1 3/4) and a whole number (2). To solve this, we'll need to convert the mixed number into an improper fraction and then apply the rules of fraction division.
Converting Mixed Numbers to Improper Fractions
A mixed number, like 1 3/4, represents a whole number plus a fraction. To convert it into an improper fraction (where the numerator is larger than the denominator), follow these steps:
- Multiply the whole number by the denominator: 1 * 4 = 4
- Add the numerator to the result: 4 + 3 = 7
- Keep the same denominator: 4
Therefore, 1 3/4 as an improper fraction is 7/4.
Dividing Fractions: The Reciprocal Method
The key to dividing fractions is understanding reciprocals. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 2/3 is 3/2. To divide fractions, we multiply the first fraction by the reciprocal of the second fraction.
Solving 1 3/4 ÷ 2 Step-by-Step
Now let's apply this knowledge to our problem:
-
Convert the mixed number to an improper fraction: As we've already established, 1 3/4 = 7/4.
-
Rewrite the division as multiplication using the reciprocal: Dividing by 2 is the same as multiplying by its reciprocal, which is 1/2. So, our problem becomes: (7/4) * (1/2)
-
Multiply the numerators and the denominators: (7 * 1) / (4 * 2) = 7/8
Therefore, 1 3/4 divided by 2 is 7/8.
Visualizing the Solution
Imagine you have a pizza cut into 8 slices. 1 3/4 pizzas would be 14 slices (7/4 of a pizza with 8 slices). If you divide those 14 slices among 2 people, each person gets 7 slices, which is 7/8 of the pizza.
Further Examples: Mastering Fraction Division
Let’s solidify your understanding with some more examples. Remember the key steps: convert mixed numbers to improper fractions, find the reciprocal of the divisor, and then multiply.
Example 1: 2 1/2 ÷ 3
- Convert 2 1/2 to an improper fraction: (2 * 2 + 1) / 2 = 5/2
- Rewrite as multiplication: (5/2) * (1/3)
- Multiply: 5/6
Therefore, 2 1/2 ÷ 3 = 5/6
Example 2: 3 1/3 ÷ 1 1/2
- Convert mixed numbers to improper fractions: 3 1/3 = 10/3; 1 1/2 = 3/2
- Rewrite as multiplication: (10/3) * (2/3)
- Multiply: 20/9 (This can also be expressed as the mixed number 2 2/9)
Therefore, 3 1/3 ÷ 1 1/2 = 20/9 or 2 2/9
Example 3: 4 ÷ 2/5
- Rewrite 4 as a fraction: 4/1
- Rewrite as multiplication: (4/1) * (5/2)
- Multiply: 20/2 = 10
Therefore, 4 ÷ 2/5 = 10
Simplifying Fractions
After performing the multiplication, always check if your answer can be simplified. A fraction is simplified when the greatest common divisor (GCD) of the numerator and denominator is 1. For example, 20/4 can be simplified to 5/1 (or simply 5) because both 20 and 4 are divisible by 4.
Troubleshooting Common Mistakes
- Forgetting to find the reciprocal: Remember, you multiply by the reciprocal of the divisor, not the divisor itself.
- Incorrect conversion of mixed numbers: Carefully follow the steps for converting mixed numbers to improper fractions. A small error here will affect the entire calculation.
- Not simplifying the final answer: Always simplify your fraction to its lowest terms for the most accurate and concise answer.
Real-World Applications
Understanding fraction division is essential in many real-world scenarios:
- Cooking: Scaling recipes up or down requires dividing fractions.
- Sewing: Calculating fabric amounts often involves fractions.
- Construction: Measuring and cutting materials accurately relies on fractional calculations.
- Data Analysis: Interpreting statistical data frequently involves working with fractions and ratios.
Conclusion: Mastering Fraction Division
Dividing fractions, including mixed numbers, might seem challenging at first, but with practice and a clear understanding of the steps involved, it becomes a manageable and even enjoyable mathematical skill. Remember the crucial steps: convert mixed numbers to improper fractions, use the reciprocal method for division, and simplify your final answer. By practicing regularly with different examples, you’ll build confidence and proficiency in this important area of mathematics. Mastering fraction division opens doors to tackling more complex mathematical problems and confidently applying this skill in various real-world situations.
Latest Posts
Latest Posts
-
In Circle C What Is The Value Of X
May 09, 2025
-
An Angle Greater Than 90 Degrees
May 09, 2025
-
How Do You Find 75 Percent Of A Number
May 09, 2025
-
If Mc021 1 Jpg And Mc021 2 Jpg What Is The Range Of Mc021 3 Jpg
May 09, 2025
-
A Number In Front Of A Variable
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 3/4 Divided By 2 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.