What Is 1 3 5 6
News Co
Apr 10, 2025 · 5 min read
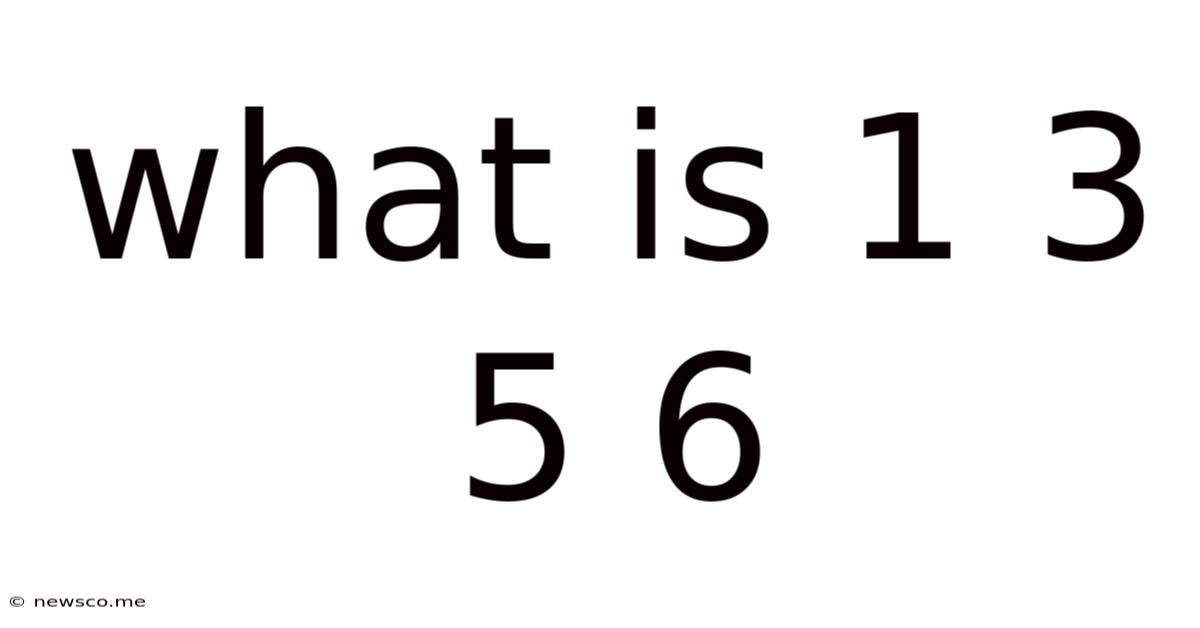
Table of Contents
What is 1 3 5 6? Unlocking the Mystery Behind Number Sequences
The seemingly simple sequence "1 3 5 6" might initially appear insignificant, a random assortment of numbers. However, a deeper dive reveals a fascinating exploration into the world of mathematics, specifically number patterns and sequences. While there isn't a single, universally accepted answer to "What is 1 3 5 6?", we can approach this question from several angles, revealing potential interpretations and underlying mathematical principles. This exploration will delve into different perspectives, including pattern recognition, mathematical operations, and even the possibility of hidden codes or puzzles.
Decoding the Sequence: Potential Interpretations
The beauty of number sequences lies in their potential for multiple interpretations. Unlike equations with fixed solutions, sequences can offer various paths towards understanding. Let's explore some potential interpretations of "1 3 5 6":
1. A Partial Sequence of Odd Numbers with a Perturbation
The numbers 1, 3, and 5 are consecutive odd numbers. The inclusion of 6 disrupts this pattern, introducing an element of irregularity. This suggests the sequence may be incomplete, or that the rule governing the sequence is more complex than simply listing odd numbers. The "6" could be a deliberate outlier, a "red herring" designed to obfuscate a simple pattern, or it could be the result of a more intricate mathematical operation.
Possible Explanations:
- Incomplete Sequence: The sequence may continue with other odd numbers, or perhaps a repeating pattern involving odd numbers and an even number. Further numbers in the sequence would be needed to confirm or refute this.
- Modified Rule: The sequence might follow a rule that incorporates both odd and even numbers in a non-obvious manner. This would require a more sophisticated mathematical expression to define.
2. A Sequence Based on Differences
Analyzing the differences between consecutive numbers can reveal hidden patterns:
- 3 - 1 = 2
- 5 - 3 = 2
- 6 - 5 = 1
The differences themselves form a sequence: 2, 2, 1. This new sequence suggests a potential rule: the difference between consecutive numbers is initially 2, then decreases by 1. However, this rule is again incomplete and doesn't readily predict subsequent numbers. To determine if this is a valid interpretation, we need additional numbers in the sequence to test this hypothesis.
3. A Combination of Arithmetic and Geometric Progressions (A Stretch)
While less likely, it’s possible to attempt more complex interpretations. We could, with some manipulation, try to fit this sequence into a system incorporating both arithmetic and geometric progressions. However, this approach will likely involve arbitrary constants and lead to complex expressions that may not provide a clear or elegant solution. The simplicity of the sequence suggests a simpler explanation is probably more accurate.
4. Prime Numbers and Composites: An Alternate Perspective
Another approach involves considering the properties of the numbers themselves.
- 1: Neither prime nor composite
- 3: Prime
- 5: Prime
- 6: Composite (2 x 3)
This perspective doesn't immediately reveal a clear pattern, but it opens the door to consider sequences based on number classifications, a common theme in number theory.
Expanding the Search: Context is Key
To better understand "1 3 5 6," we need more context. Where did this sequence originate? Is it part of a larger problem, a puzzle, or a code? The source of the sequence is crucial. For example:
- Puzzle or Riddle: If this sequence is part of a larger puzzle or riddle, the context provided within the puzzle will provide critical clues to its meaning. The sequence may be a key, a code, or a piece of information leading to a solution.
- Mathematical Problem: If the sequence comes from a mathematical problem, the problem statement will contain vital information about the rules governing the sequence.
- Real-world Data: The sequence could represent some real-world data, such as measurements, observations, or events. Without understanding the underlying process generating this data, deciphering the meaning of the sequence becomes difficult.
Applying Mathematical Tools for Analysis
While intuition and observation are crucial, formal mathematical tools can aid in analyzing number sequences. These include:
- Recursive Formulas: This method expresses each term in the sequence as a function of previous terms. For "1 3 5 6," creating a recursive formula is challenging due to the irregular nature of the sequence.
- Generating Functions: Generating functions provide a way to represent an infinite sequence as a single mathematical function. However, it's unlikely that "1 3 5 6" on its own will lead to a meaningful generating function without additional terms.
- Difference Tables: As mentioned earlier, analyzing the differences between consecutive terms can unveil hidden patterns. Creating a difference table involves calculating the differences between consecutive terms, then the differences between those differences, and so on. The pattern in the difference table might reveal a more straightforward rule.
Beyond Simple Sequences: Exploring Deeper Concepts
The apparent simplicity of "1 3 5 6" shouldn't mislead us. The search for meaning in number sequences opens doors to deeper mathematical concepts, including:
- Fibonacci Sequence: While "1 3 5 6" isn't directly related to the Fibonacci sequence (1, 1, 2, 3, 5, 8...), it highlights the importance of recognizing patterns within seemingly random sequences.
- Catalan Numbers: These numbers appear in various combinatorial problems, and while unrelated to this specific sequence, they showcase the vast applications of mathematical sequences in problem-solving.
- Recursive Sequences and Iterative Processes: The search for a rule governing "1 3 5 6" naturally leads to the study of recursive sequences and iterative processes, essential in computer science and many areas of mathematics.
The Importance of Context and Further Investigation
In conclusion, the question "What is 1 3 5 6?" doesn't have a single definitive answer without more information. The sequence's ambiguity highlights the importance of context in interpreting mathematical patterns. While several potential interpretations exist, none definitively explain the sequence's origin or underlying rule. To unravel the mystery, additional data or context surrounding the sequence is crucial. This exploration, however, showcases the power of mathematical thinking, emphasizing the need for critical analysis, pattern recognition, and the application of various mathematical tools. Further investigation and a richer context are vital for finding a conclusive answer, transforming a simple sequence into a fascinating mathematical puzzle. The search itself underscores the rewarding aspects of mathematical exploration and the inherent beauty of seemingly simple number sequences.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 1 3 5 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.