What Is 1 3 Of 1 1 2
News Co
Mar 24, 2025 · 5 min read
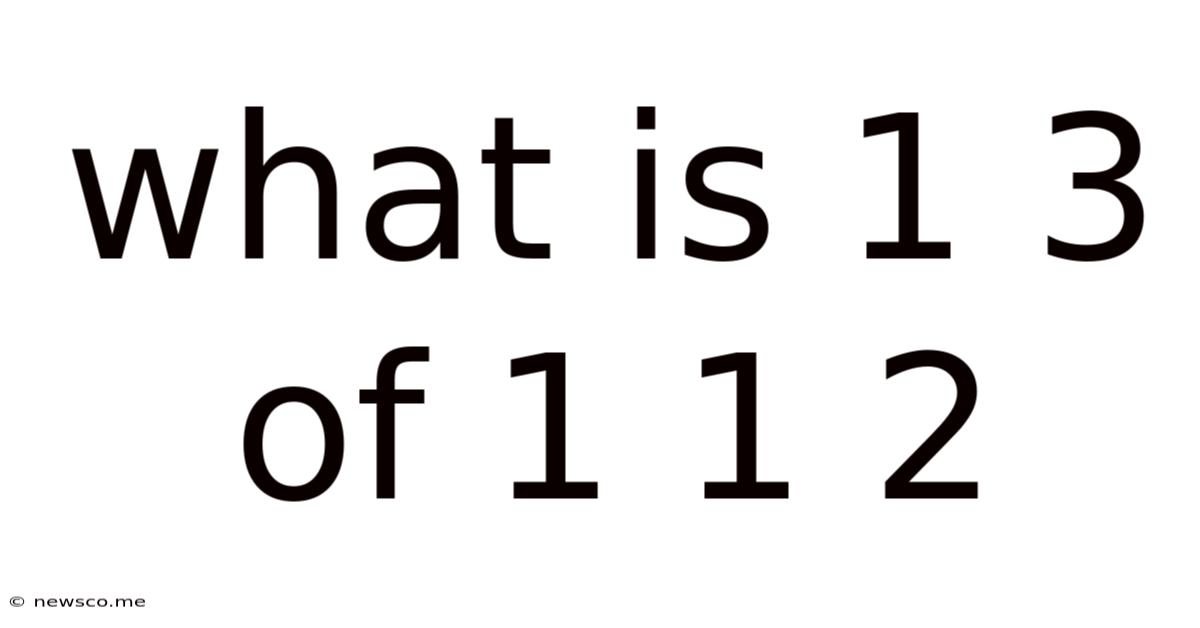
Table of Contents
What is 1/3 of 1 1/2? A Deep Dive into Fractions and Their Applications
This seemingly simple question, "What is 1/3 of 1 1/2?", opens the door to a fascinating exploration of fractions, their manipulation, and their wide-ranging applications in everyday life and various fields. While the answer itself is straightforward, understanding the underlying principles and methods involved is crucial for building a strong foundation in mathematics and problem-solving.
Understanding Fractions: A Building Block of Mathematics
Before we tackle the specific problem, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two key parts:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For instance, in the fraction 1/3, the numerator (1) signifies we have one part, and the denominator (3) signifies the whole is divided into three equal parts.
Converting Mixed Numbers to Improper Fractions
Our problem involves a mixed number, 1 1/2. A mixed number combines a whole number and a fraction. To work with it efficiently in calculations involving other fractions, we need to convert it into an improper fraction. An improper fraction has a numerator larger than or equal to its denominator.
Here's how to convert 1 1/2 to an improper fraction:
- Multiply the whole number by the denominator: 1 * 2 = 2
- Add the numerator to the result: 2 + 1 = 3
- Keep the same denominator: 2
Therefore, 1 1/2 is equivalent to the improper fraction 3/2.
Calculating 1/3 of 3/2: The Multiplication Process
Now that we've converted 1 1/2 to an improper fraction, we can proceed with the calculation: What is 1/3 of 3/2? In mathematical terms, this translates to:
(1/3) * (3/2)
Multiplying fractions is straightforward:
- Multiply the numerators: 1 * 3 = 3
- Multiply the denominators: 3 * 2 = 6
This gives us the fraction 3/6.
Simplifying Fractions: Reducing to the Lowest Terms
The fraction 3/6 is not in its simplest form. To simplify, we find the greatest common divisor (GCD) of the numerator and denominator. The GCD of 3 and 6 is 3. We then divide both the numerator and denominator by the GCD:
3 ÷ 3 = 1 6 ÷ 3 = 2
This simplifies 3/6 to 1/2.
Therefore, 1/3 of 1 1/2 is 1/2.
Real-World Applications of Fraction Calculations
The seemingly simple calculation above has far-reaching implications in various real-world scenarios:
-
Cooking and Baking: Recipes often require fractional measurements of ingredients. Understanding fraction operations is crucial for accurate measurements and successful cooking. For example, if a recipe calls for 1 1/2 cups of flour and you only want to make 1/3 of the recipe, knowing that 1/3 of 1 1/2 cups is 1/2 cup is essential.
-
Construction and Engineering: Precise measurements and calculations are paramount in construction and engineering. Fractions are used extensively in blueprints, measurements, and material calculations. Understanding fraction manipulation ensures accuracy and precision in these fields. Imagine calculating the amount of material needed for a project that requires a fractional portion of a standard unit.
-
Finance and Economics: Fractions are integral to financial calculations, including interest rates, percentages, and stock market analysis. Understanding fractional calculations is essential for making sound financial decisions. For instance, determining the fractional portion of an investment’s return or calculating discounts.
-
Data Analysis and Statistics: Fractions and percentages are frequently used in representing data and performing statistical analysis. Understanding fractional representations helps in interpreting and drawing conclusions from data sets.
-
Science and Technology: Many scientific and technological applications involve measurements and calculations using fractions. From physics experiments to computer programming, fractions play a significant role. For example, in determining ratios or proportions in a chemical reaction.
Expanding on Fraction Operations: Beyond the Basics
While this article focused on a specific problem, understanding fractions goes far beyond simple multiplication. Here's a brief overview of other crucial fraction operations:
-
Addition and Subtraction: Adding and subtracting fractions requires a common denominator. If the fractions have different denominators, you must find a common multiple and convert the fractions before performing the operation.
-
Division: Dividing fractions involves inverting the second fraction (the divisor) and then multiplying.
-
Converting Fractions to Decimals and Percentages: Fractions can be easily converted to decimals by dividing the numerator by the denominator. Decimals can then be expressed as percentages by multiplying by 100. This allows for different ways to represent the same quantity.
-
Solving Equations with Fractions: Fractions frequently appear in algebraic equations. Solving these equations often involves manipulating fractions using the methods discussed above.
Mastering Fractions: A Continuous Learning Process
The ability to work confidently with fractions is a fundamental skill with wide-ranging applications. While the initial steps might seem challenging, consistent practice and a solid understanding of the underlying principles will build confidence and proficiency. This knowledge serves as a cornerstone for further mathematical advancements and problem-solving in numerous fields. This seemingly simple question, “What is 1/3 of 1 1/2?”, provides a starting point for a much broader and essential understanding of mathematical principles applicable in various facets of life. From calculating ingredients for a recipe to understanding complex financial models, the mastery of fractions remains a valuable skill for lifelong learning and problem-solving. The process of converting mixed numbers, performing the multiplication, and simplifying the resulting fraction highlight the importance of step-by-step calculation and attention to detail in mathematical problem-solving. Remember, the ability to confidently and accurately perform calculations with fractions forms the foundation for more advanced mathematical concepts and their real-world applications.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 1 3 Of 1 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.