What Is 1 3 Of 2 1 2
News Co
Apr 11, 2025 · 5 min read
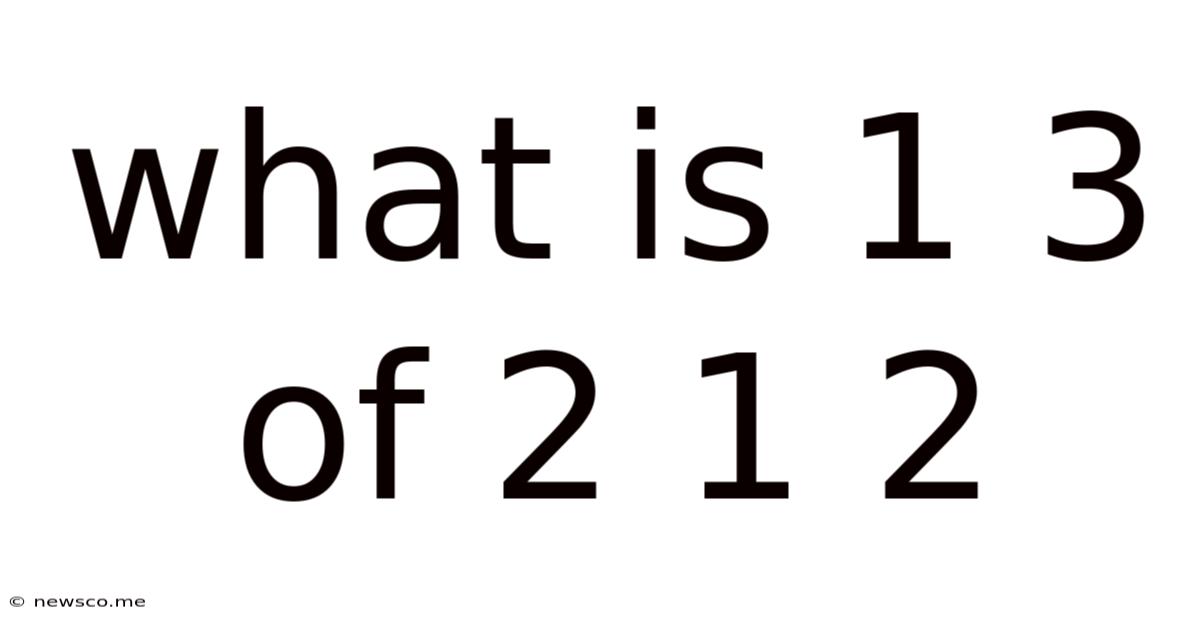
Table of Contents
What is 1/3 of 2 1/2? A Comprehensive Guide to Fraction Multiplication
Understanding fractions and how to perform operations like multiplication with them is a fundamental skill in mathematics. This comprehensive guide will walk you through the process of calculating 1/3 of 2 1/2, explaining the underlying concepts and providing various methods to arrive at the solution. We’ll delve into the theory, provide step-by-step instructions, and offer helpful tips to improve your understanding of fraction manipulation.
Understanding the Problem: 1/3 of 2 1/2
The phrase "1/3 of 2 1/2" translates mathematically to the multiplication problem: (1/3) * (2 1/2). This involves multiplying a fraction (1/3) by a mixed number (2 1/2). Before we begin the calculation, let's review some key concepts.
Key Concepts: Fractions and Mixed Numbers
-
Fractions: A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many parts make up the whole.
-
Mixed Numbers: A mixed number combines a whole number and a fraction. For example, 2 1/2 means two whole units and one-half of a unit.
-
Improper Fractions: An improper fraction is a fraction where the numerator is greater than or equal to the denominator. For example, 5/2 is an improper fraction.
Method 1: Converting to Improper Fractions
This is the most common and generally preferred method for multiplying fractions involving mixed numbers. It involves converting the mixed number into an improper fraction before performing the multiplication.
Step 1: Convert the Mixed Number to an Improper Fraction
To convert 2 1/2 to an improper fraction, we multiply the whole number (2) by the denominator (2) and add the numerator (1). This result becomes the new numerator, and the denominator remains the same.
2 1/2 = (2 * 2 + 1) / 2 = 5/2
Step 2: Multiply the Fractions
Now we multiply the two fractions: (1/3) * (5/2)
To multiply fractions, we multiply the numerators together and the denominators together:
(1 * 5) / (3 * 2) = 5/6
Therefore, 1/3 of 2 1/2 is 5/6.
Method 2: Distributive Property
The distributive property of multiplication allows us to break down the problem into smaller, more manageable parts. This method is particularly useful when dealing with larger mixed numbers.
Step 1: Separate the Mixed Number
We can rewrite 2 1/2 as 2 + 1/2.
Step 2: Apply the Distributive Property
Now, we apply the distributive property:
(1/3) * (2 + 1/2) = (1/3) * 2 + (1/3) * (1/2)
Step 3: Perform the Multiplications
(1/3) * 2 = 2/3
(1/3) * (1/2) = 1/6
Step 4: Add the Results
Now we add the results together:
2/3 + 1/6
To add these fractions, we need a common denominator, which is 6. We convert 2/3 to an equivalent fraction with a denominator of 6:
(2/3) * (2/2) = 4/6
Now we add:
4/6 + 1/6 = 5/6
Again, we arrive at the answer: 5/6
Method 3: Using Decimal Representation
While not always ideal for maintaining accuracy, especially with complex fractions, we can convert the fractions to decimals for a quicker calculation.
Step 1: Convert Fractions to Decimals
1/3 ≈ 0.3333 (recurring decimal)
2 1/2 = 2.5
Step 2: Perform Decimal Multiplication
0.3333 * 2.5 ≈ 0.8333
Step 3: Convert Back to a Fraction (if necessary)
This decimal, 0.8333, is approximately equal to 5/6. Note that this method introduces a slight approximation due to the recurring decimal nature of 1/3.
Visual Representation
Imagine a pizza cut into six slices. Two and a half pizzas would be fifteen slices (2.5 * 6 = 15). One-third of these fifteen slices is five slices (15/3 = 5). Therefore, one-third of two and a half pizzas is 5/6 of a pizza.
Practical Applications
Understanding fraction multiplication has numerous practical applications in everyday life and various fields:
- Cooking and Baking: Scaling recipes up or down often requires multiplying fractions.
- Construction and Engineering: Precise measurements and calculations frequently involve fractions.
- Finance and Budgeting: Working with percentages and proportions necessitates fraction manipulation.
- Science and Data Analysis: Many scientific calculations rely on accurate fraction calculations.
Troubleshooting and Common Mistakes
- Forgetting to convert mixed numbers to improper fractions: This is a common mistake that leads to incorrect answers. Always convert mixed numbers to improper fractions before multiplying.
- Incorrectly multiplying numerators and denominators: Double-check your multiplication to avoid errors.
- Not simplifying the final answer: Always simplify the resulting fraction to its lowest terms.
Further Exploration: More Complex Fraction Problems
Once you've mastered the basics of multiplying fractions, you can move on to more advanced problems involving:
- Multiplying three or more fractions
- Multiplying fractions by decimals
- Solving word problems involving fractions
- Understanding fraction division
Conclusion: Mastering Fraction Multiplication
Understanding how to calculate 1/3 of 2 1/2, and more broadly, how to perform fraction multiplication, is a crucial mathematical skill. By mastering these techniques, you’ll be equipped to handle various real-world situations that require accurate fraction calculations. Remember to practice consistently, utilize the methods described above, and break down complex problems into smaller, more manageable steps. With practice, you’ll build confidence and fluency in working with fractions. The key is to understand the underlying concepts and to choose the method that best suits your understanding and the complexity of the problem.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 1 3 Of 2 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.