What Is 1 3 Of 6
News Co
Mar 20, 2025 · 5 min read
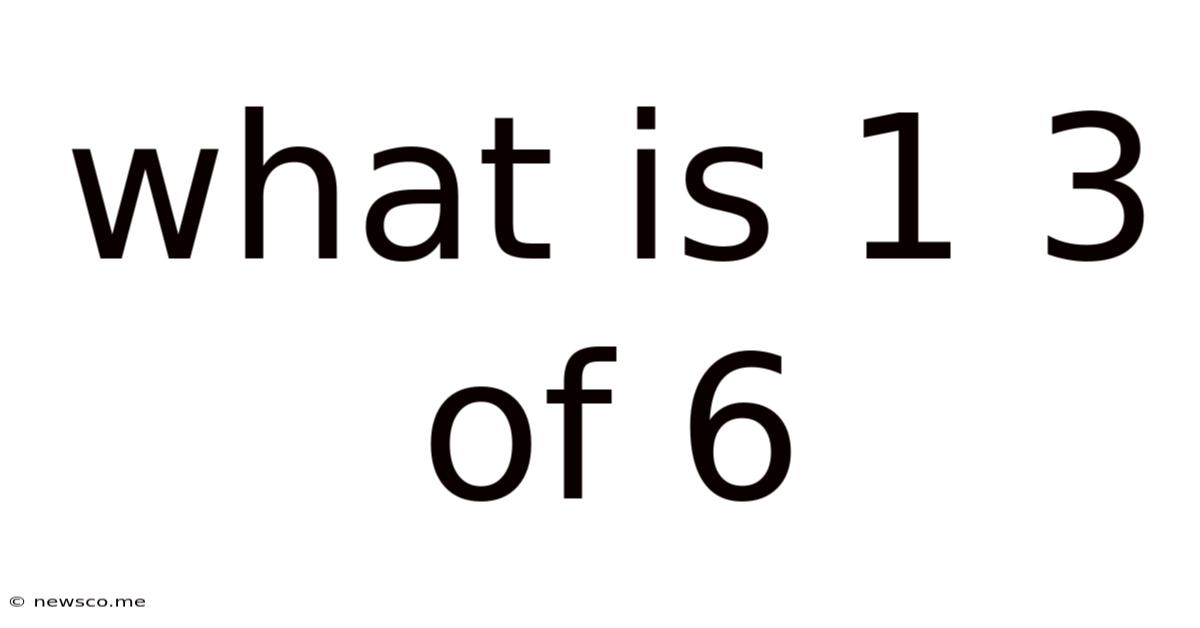
Table of Contents
What is 1/3 of 6? A Comprehensive Guide to Fractions and Their Applications
Finding a fraction of a whole number might seem like a simple arithmetic problem, but understanding the underlying concepts is crucial for mastering more complex mathematical operations. This comprehensive guide will not only answer the question "What is 1/3 of 6?" but also delve into the principles of fractions, offering practical examples and applications in various fields.
Understanding Fractions: A Foundation
Before we tackle the specific problem, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator specifies how many of those parts we're considering.
For example, in the fraction 1/3, the denominator 3 means the whole is divided into three equal parts. The numerator 1 indicates we're looking at one of those three parts.
Key Concepts in Fraction Arithmetic
Several essential concepts underpin fraction calculations:
-
Simplifying Fractions: This involves reducing a fraction to its simplest form by dividing both the numerator and denominator by their greatest common divisor (GCD). For example, 6/9 simplifies to 2/3 because the GCD of 6 and 9 is 3.
-
Equivalent Fractions: These are fractions that represent the same value, even though they have different numerators and denominators. For instance, 1/2, 2/4, and 3/6 are all equivalent fractions.
-
Adding and Subtracting Fractions: To add or subtract fractions, they must have a common denominator. If they don't, you need to find the least common multiple (LCM) of the denominators and convert the fractions accordingly.
-
Multiplying Fractions: Multiplying fractions is straightforward: multiply the numerators together and the denominators together. Simplification is often possible after multiplication.
-
Dividing Fractions: Dividing by a fraction is the same as multiplying by its reciprocal (inverting the fraction).
Solving the Problem: What is 1/3 of 6?
Now, let's address the central question: "What is 1/3 of 6?"
This can be solved in two primary ways:
Method 1: Multiplication
Finding a fraction of a number is equivalent to multiplying the fraction by the number. Therefore, to find 1/3 of 6, we perform the multiplication:
(1/3) * 6 = 6/3
This fraction can be simplified by dividing both the numerator and the denominator by their GCD, which is 3:
6/3 = 2
Therefore, 1/3 of 6 is 2.
Method 2: Division
Alternatively, we can solve this using division. Since we want to find one-third of 6, we divide 6 into three equal parts:
6 ÷ 3 = 2
This also confirms that 1/3 of 6 is 2.
Real-World Applications of Fractions
Fractions are not just abstract mathematical concepts; they have widespread applications in daily life and various professions. Here are some examples:
Cooking and Baking
Recipes often involve fractions. For instance, a recipe might call for 2/3 cup of flour or 1/4 teaspoon of salt. Understanding fractions is essential for accurate measurement and successful cooking.
Construction and Engineering
Fractions are critical in construction and engineering projects. Blueprints and designs often use fractional measurements for precise construction. Engineers use fractions to calculate structural loads, material quantities, and dimensions.
Finance and Business
Fractions play a significant role in finance. Interest rates, stock prices, and financial ratios are often expressed as fractions or decimals (which are essentially fractions). Understanding fractions is crucial for making informed financial decisions.
Science and Medicine
Fractions are used extensively in scientific measurements and experiments. Scientists use fractions to represent concentrations, ratios, and proportions. In medicine, dosages of medication are frequently expressed as fractions.
Data Analysis and Statistics
Fractions and percentages (which are a type of fraction) are fundamental tools for data analysis and statistics. Representing data using fractions helps in visualizing proportions and relationships within datasets.
Expanding on Fraction Concepts: Mixed Numbers and Improper Fractions
Beyond the basic understanding of fractions, let's explore two related concepts:
Mixed Numbers
A mixed number combines a whole number and a proper fraction (a fraction where the numerator is smaller than the denominator). For instance, 2 1/2 is a mixed number.
To convert a mixed number to an improper fraction (a fraction where the numerator is larger than or equal to the denominator), multiply the whole number by the denominator, add the numerator, and keep the same denominator. So, 2 1/2 becomes (2*2 + 1)/2 = 5/2.
Improper Fractions
Improper fractions, as mentioned above, have a numerator greater than or equal to the denominator. They can be converted to mixed numbers by dividing the numerator by the denominator. The quotient becomes the whole number, and the remainder becomes the numerator of the fraction part.
For example, converting 7/3 to a mixed number: 7 ÷ 3 = 2 with a remainder of 1. Thus, 7/3 is equivalent to 2 1/3.
Advanced Applications: Fractions in Algebra and Calculus
The principles of fractions extend far beyond basic arithmetic. They form the foundation for more advanced mathematical concepts:
Algebra
Solving algebraic equations often involves working with fractions. Manipulating fractional expressions is a key skill in algebra.
Calculus
Calculus, the study of change, relies heavily on the concept of limits, which often involve working with increasingly small fractions. Derivatives and integrals, fundamental concepts in calculus, frequently incorporate fractional expressions.
Conclusion: Mastering Fractions for a Broader Understanding
This comprehensive guide has not only answered the question "What is 1/3 of 6?" but also provided a thorough exploration of fractions and their wide-ranging applications. Understanding fractions is a cornerstone of mathematical literacy and has practical relevance across many disciplines. By grasping the concepts discussed here – simplifying fractions, finding equivalent fractions, performing operations with fractions, and understanding mixed numbers and improper fractions – you will be well-equipped to tackle more complex mathematical problems and succeed in various fields where fractional calculations are essential. Remember, the ability to work confidently with fractions is a crucial skill that builds a strong foundation for future mathematical learning and real-world problem-solving.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 1 3 Of 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.