What Is 1 3 Plus 1 3 Equal
News Co
Apr 18, 2025 · 5 min read
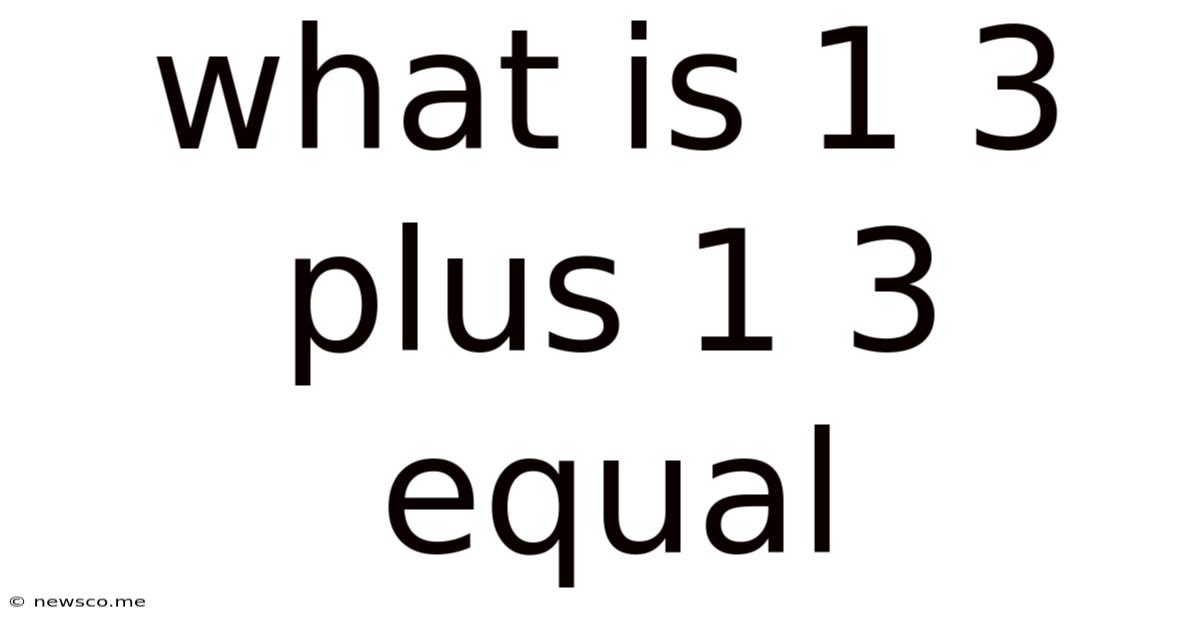
Table of Contents
What is 1/3 Plus 1/3 Equal? A Deep Dive into Fraction Addition
The seemingly simple question, "What is 1/3 plus 1/3 equal?" opens the door to a deeper understanding of fractions, a fundamental concept in mathematics. While the answer itself is straightforward, exploring the underlying principles and extending the concept to more complex scenarios provides valuable insight for students and anyone looking to strengthen their mathematical foundation. This comprehensive guide will dissect this seemingly simple problem, exploring various approaches and offering practical applications.
Understanding Fractions: The Building Blocks
Before we delve into the addition, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator shows how many of those parts are being considered.
For example, in the fraction 1/3, the denominator (3) signifies that the whole is divided into three equal parts, and the numerator (1) indicates that we're considering only one of those parts.
Key Terminology:
- Numerator: The top number in a fraction.
- Denominator: The bottom number in a fraction.
- Proper Fraction: A fraction where the numerator is smaller than the denominator (e.g., 1/3, 2/5).
- Improper Fraction: A fraction where the numerator is equal to or larger than the denominator (e.g., 5/3, 7/2).
- Mixed Number: A number consisting of a whole number and a proper fraction (e.g., 1 2/3).
Adding Fractions with the Same Denominator
The beauty of adding fractions with identical denominators lies in its simplicity. Since the fractions represent parts of the same whole, we simply add the numerators while keeping the denominator unchanged.
The Rule: To add fractions with the same denominator, add the numerators and keep the denominator the same.
Let's apply this to our problem: 1/3 + 1/3
- Add the numerators: 1 + 1 = 2
- Keep the denominator the same: 3
Therefore, 1/3 + 1/3 = 2/3
This means that if you have one-third of a pizza and you add another one-third of a pizza, you now have two-thirds of a pizza.
Visualizing the Addition
Visual representations can significantly aid in understanding fraction addition. Imagine a circle divided into three equal parts. Shading one part represents 1/3. Shading another part represents another 1/3. Together, the shaded portions represent 2/3 of the circle. This visual reinforces the concept that adding fractions with like denominators is simply combining the parts.
Extending the Concept: Adding More Fractions with the Same Denominator
The principle extends easily to adding more than two fractions with the same denominator. Simply add all the numerators and retain the common denominator.
For instance: 1/5 + 2/5 + 1/5 = (1 + 2 + 1)/5 = 4/5
Adding Fractions with Different Denominators: Finding a Common Denominator
Adding fractions with different denominators requires an extra step: finding a common denominator. A common denominator is a number that is a multiple of both denominators. The process involves finding the least common multiple (LCM) of the denominators.
Let's illustrate with an example: 1/2 + 1/3
-
Find the LCM of the denominators (2 and 3): The LCM of 2 and 3 is 6.
-
Convert the fractions to equivalent fractions with the common denominator (6):
- 1/2 = (1 x 3)/(2 x 3) = 3/6
- 1/3 = (1 x 2)/(3 x 2) = 2/6
-
Add the fractions: 3/6 + 2/6 = (3 + 2)/6 = 5/6
Therefore, 1/2 + 1/3 = 5/6
Simplifying Fractions: Reducing to Lowest Terms
After adding fractions, it's often necessary to simplify the result by reducing it to its lowest terms. This involves dividing both the numerator and denominator by their greatest common divisor (GCD).
For example, the fraction 4/6 can be simplified:
-
Find the GCD of 4 and 6: The GCD of 4 and 6 is 2.
-
Divide both the numerator and denominator by the GCD: 4/2 = 2 and 6/2 = 3
Therefore, 4/6 simplified is 2/3. This demonstrates that 4/6 and 2/3 represent the same value.
Real-World Applications of Fraction Addition
Understanding fraction addition extends beyond the classroom. It has practical applications in various aspects of life:
-
Cooking and Baking: Recipes often require fractional amounts of ingredients. Adding fractions helps determine the total amount of an ingredient needed.
-
Construction and Engineering: Precise measurements are critical in construction and engineering. Fraction addition is used to calculate total lengths, areas, and volumes.
-
Finance: Dealing with parts of a whole, such as portions of investments or interest calculations, frequently involves fraction addition.
-
Data Analysis: Representing and manipulating data often uses fractions and their addition.
Improper Fractions and Mixed Numbers
When the result of adding fractions is an improper fraction (numerator greater than or equal to the denominator), it's common practice to convert it into a mixed number. A mixed number represents a whole number and a fraction.
For example, the improper fraction 7/3 can be converted to a mixed number:
-
Divide the numerator (7) by the denominator (3): 7 ÷ 3 = 2 with a remainder of 1.
-
The quotient (2) becomes the whole number part, and the remainder (1) becomes the numerator of the fractional part. The denominator remains the same (3).
Therefore, 7/3 = 2 1/3
Advanced Concepts and Further Exploration
This exploration of fraction addition provides a solid foundation. However, the topic expands into more advanced concepts:
-
Adding more than two fractions with different denominators: The principles remain the same; find the LCM of all denominators and convert the fractions before adding.
-
Adding fractions and decimals: Decimals can be converted to fractions for addition.
-
Algebraic fractions: Fractions containing variables are handled similarly, focusing on finding common denominators and simplifying.
Conclusion: Mastering the Fundamentals
Understanding what 1/3 plus 1/3 equals is a stepping stone to a more profound understanding of fractions and their applications. By mastering the fundamentals, including finding common denominators, simplifying fractions, and converting between improper fractions and mixed numbers, one can tackle more complex mathematical problems and confidently apply these skills in various real-world scenarios. The seemingly simple addition of 1/3 and 1/3 provides a gateway to a wealth of mathematical knowledge and problem-solving capabilities.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 1 3 Plus 1 3 Equal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.