What Is 1 5 Of 1 2
News Co
Apr 10, 2025 · 4 min read
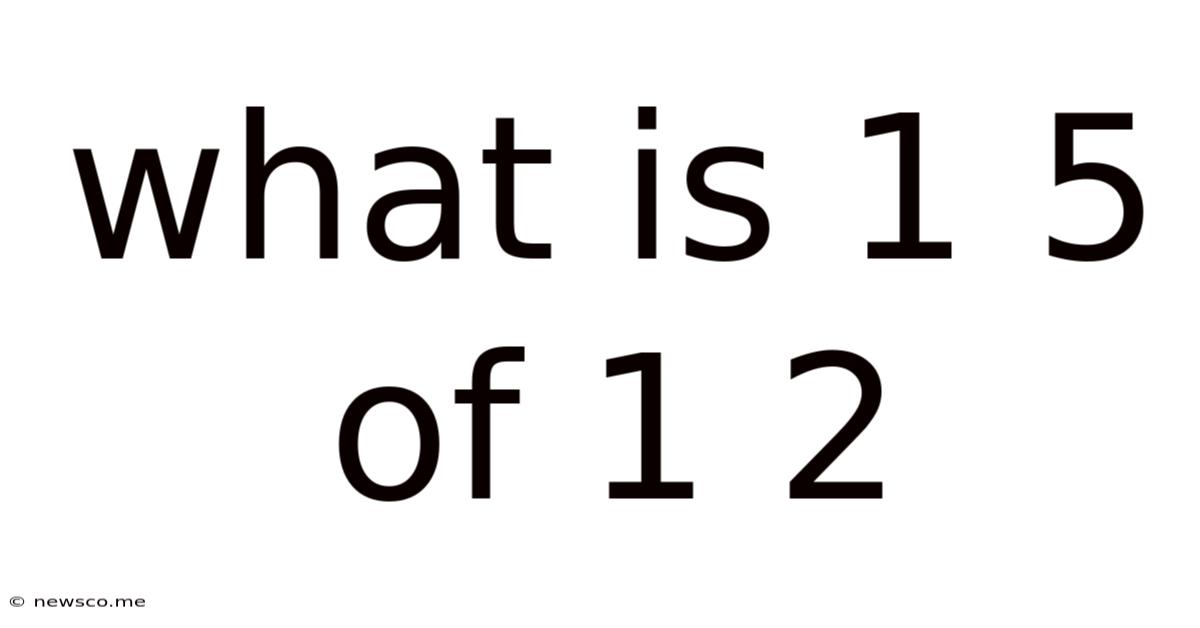
Table of Contents
What is 1/5 of 1/2? A Comprehensive Guide to Fractions and Their Applications
Understanding fractions is fundamental to mathematics and numerous real-world applications. This article delves into the question, "What is 1/5 of 1/2?", providing a step-by-step explanation, exploring various methods of solving fraction problems, and demonstrating the practical relevance of fractions in everyday life. We'll also touch upon the broader mathematical concepts involved and explore how to confidently tackle similar fraction problems.
Understanding Fractions: A Refresher
Before we tackle the core problem, let's revisit the basics of fractions. A fraction represents a part of a whole. It consists of two key components:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating how many equal parts the whole is divided into.
For example, in the fraction 1/2 (one-half), the numerator is 1 and the denominator is 2. This signifies one part out of two equal parts.
Solving "What is 1/5 of 1/2?"
The phrase "1/5 of 1/2" implies multiplication. To find 1/5 of 1/2, we simply multiply the two fractions together:
(1/5) x (1/2) = ?
Method 1: Multiplying Numerators and Denominators
The most straightforward method is to multiply the numerators together and the denominators together separately:
- Multiply the numerators: 1 x 1 = 1
- Multiply the denominators: 5 x 2 = 10
Therefore, (1/5) x (1/2) = 1/10
Method 2: Visual Representation
Imagine a rectangle representing one whole unit. Divide it into two equal halves (representing 1/2). Now, take one of those halves and divide that into five equal parts (representing 1/5 of 1/2). You'll find that the resulting piece is one-tenth of the original whole rectangle. This visual approach reinforces the mathematical result.
Expanding on Fraction Operations: Beyond Multiplication
While the primary focus is on solving "1/5 of 1/2," it's crucial to understand other fraction operations to handle more complex problems. These include:
Addition and Subtraction of Fractions
Adding or subtracting fractions requires a common denominator. If the denominators are the same, simply add or subtract the numerators and keep the denominator constant. If the denominators are different, you must find the least common multiple (LCM) of the denominators and convert the fractions to equivalent fractions with the LCM as the denominator.
Example: 1/3 + 1/6
The LCM of 3 and 6 is 6. We convert 1/3 to 2/6:
2/6 + 1/6 = 3/6 = 1/2
Division of Fractions
Dividing fractions involves inverting the second fraction (the divisor) and multiplying.
Example: (1/2) ÷ (1/4)
1/2 x 4/1 = 4/2 = 2
Real-World Applications of Fractions
Fractions are not just abstract mathematical concepts; they are essential tools in everyday life. Here are some examples:
- Cooking and Baking: Recipes frequently use fractions (e.g., 1/2 cup of sugar, 1/4 teaspoon of salt).
- Measurement: Measuring lengths, weights, and volumes often involves fractions (e.g., 2 1/2 inches, 3/4 pound).
- Finance: Understanding fractions is crucial for managing budgets, calculating percentages, and working with interest rates.
- Construction: Fractions are integral to blueprints, measurements, and material calculations.
- Data Analysis: Representing parts of a whole in data sets often utilizes fractions or percentages (which are derived from fractions).
Advanced Concepts Related to Fractions
For those seeking a deeper understanding, here are some advanced topics related to fractions:
- Improper Fractions and Mixed Numbers: An improper fraction has a numerator larger than its denominator (e.g., 5/4). A mixed number combines a whole number and a fraction (e.g., 1 1/4). These forms are interchangeable.
- Simplifying Fractions: Reducing a fraction to its simplest form involves dividing both the numerator and denominator by their greatest common divisor (GCD). This makes the fraction easier to understand and work with.
- Decimal Representation: Fractions can be expressed as decimals by dividing the numerator by the denominator.
- Percentage Conversion: Fractions can be easily converted to percentages by multiplying by 100%.
Tackling Similar Fraction Problems: A Step-by-Step Approach
To effectively solve similar problems involving fractions, follow these steps:
- Identify the operation: Determine whether the problem requires addition, subtraction, multiplication, or division.
- Find a common denominator (if necessary): For addition and subtraction, ensure the fractions have the same denominator before proceeding.
- Perform the operation: Carry out the appropriate calculation (addition, subtraction, multiplication, or division).
- Simplify the result: Reduce the fraction to its simplest form if possible.
Conclusion: Mastering Fractions for Everyday Success
Understanding fractions is a cornerstone of mathematical literacy. While the seemingly simple question, "What is 1/5 of 1/2?", serves as an excellent starting point, it opens the door to a world of mathematical applications impacting various aspects of our lives. By mastering the fundamental operations of fractions and exploring their real-world significance, you equip yourself with valuable skills for academic success, professional advancement, and informed decision-making in everyday scenarios. Remember to practice regularly, and don't hesitate to explore additional resources for a deeper understanding of this essential mathematical concept. Through consistent effort, you can confidently navigate the world of fractions and unlock their potential in solving everyday problems.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 1 5 Of 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.