What Is 1.5 Percent Of 100
News Co
Apr 13, 2025 · 4 min read
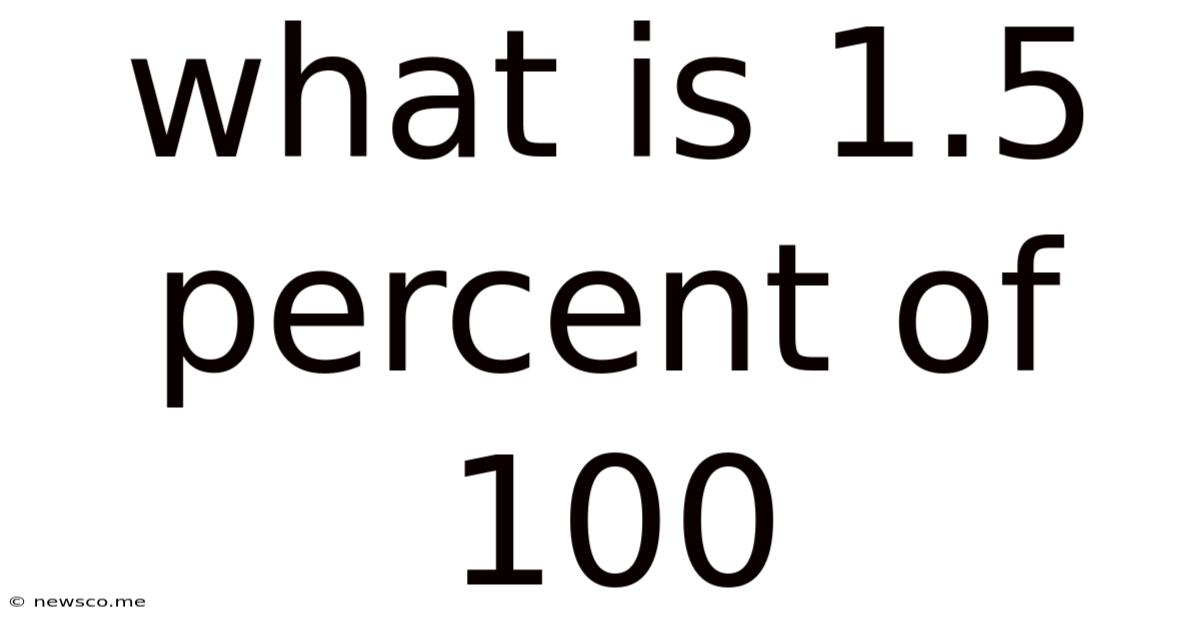
Table of Contents
What is 1.5 Percent of 100? A Deep Dive into Percentages and Their Applications
Calculating percentages is a fundamental skill with wide-ranging applications in various aspects of life, from everyday budgeting to complex financial analyses. Understanding how to determine percentages is crucial for making informed decisions and navigating numerous situations. This article delves into the seemingly simple question, "What is 1.5 percent of 100?", and expands upon the broader context of percentage calculations, exploring different methods, real-world examples, and practical applications.
Understanding Percentages: The Basics
Before we tackle the specific calculation, let's refresh our understanding of percentages. A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of one hundred" (per centum in Latin). Therefore, 1% represents 1/100, 50% represents 50/100 (or 1/2), and 100% represents 100/100 (or 1).
Key Concepts:
- The Whole: This is the total amount you're considering. In our example, the whole is 100.
- The Part: This is the portion of the whole you're interested in finding. In our case, we want to find 1.5% of the whole.
- The Percentage: This is the rate expressed as a fraction of 100. In our example, the percentage is 1.5%.
Calculating 1.5 Percent of 100: Three Methods
There are several ways to calculate 1.5% of 100. Let's explore three common methods:
Method 1: Using the Decimal Equivalent
This is arguably the most straightforward method. To use this method, we first convert the percentage to its decimal equivalent. To do this, divide the percentage by 100:
1.5% ÷ 100 = 0.015
Now, multiply the decimal equivalent by the whole number:
0.015 x 100 = 1.5
Therefore, 1.5% of 100 is 1.5.
Method 2: Using Fractions
We can also approach this problem using fractions. Remember that 1.5% can be written as 1.5/100. Then, we can set up the calculation as follows:
(1.5/100) x 100
The 100s cancel out, leaving us with:
1.5
Again, we find that 1.5% of 100 is 1.5.
Method 3: Proportions
This method involves setting up a proportion. We know that 100% represents 100, and we want to find the value that corresponds to 1.5%. We can set up the proportion as follows:
100%/100 = 1.5%/x
To solve for x (which represents 1.5% of 100), we cross-multiply:
100x = 1.5 * 100
100x = 150
x = 150/100
x = 1.5
Once again, we arrive at the answer: 1.5% of 100 is 1.5.
Real-World Applications of Percentage Calculations
The ability to calculate percentages has countless practical applications. Here are just a few examples:
1. Financial Calculations:
- Interest Rates: Calculating simple and compound interest on loans, savings accounts, and investments heavily relies on percentage calculations. Understanding interest rates is vital for making informed financial decisions. For example, if you have a savings account with a 1.5% annual interest rate and a balance of $100, you'd earn $1.50 in interest after one year.
- Discounts and Sales Tax: Retailers frequently offer discounts as percentages. Knowing how to calculate percentages allows you to quickly determine the final price after a discount. Similarly, understanding sales tax percentages is crucial for budgeting and determining the total cost of purchases.
- Investment Returns: Investors use percentage calculations to track the performance of their investments. Calculating percentage changes in investment values helps assess profitability and risk.
- Budgeting and Expense Tracking: Understanding percentages is vital for effective budgeting. You can track your expenses as percentages of your income to identify areas for potential savings.
2. Scientific and Statistical Analysis:
- Data Representation: Percentages are commonly used to represent data in charts, graphs, and tables, making complex information more accessible and understandable.
- Probability and Statistics: Percentages are integral to probability and statistical analysis. For example, expressing the likelihood of an event occurring as a percentage is a common practice.
- Scientific Experiments: Scientists use percentages to represent the results of experiments and studies. For example, the success rate of a treatment might be expressed as a percentage.
3. Everyday Life:
- Tipping: Calculating tips in restaurants is a common application of percentage calculations.
- Surveys and Polls: Results of surveys and polls are often expressed as percentages to summarize the opinions of a larger group.
- Grading Systems: Many educational systems use percentages to represent student grades.
Beyond the Basics: Working with More Complex Percentages
While our example dealt with a relatively simple percentage calculation, the principles extend to more complex scenarios. For instance, calculating a percentage of a percentage or working with larger or smaller numbers follows the same fundamental principles. The key is to accurately convert percentages to decimals or fractions and apply the correct mathematical operations.
Conclusion
Calculating 1.5% of 100, as we've demonstrated, results in 1.5. While seemingly straightforward, this simple calculation highlights the broader importance of understanding percentages. From managing personal finances to analyzing complex data sets, the ability to calculate and interpret percentages is an essential skill across numerous disciplines and everyday life. Mastering percentage calculations empowers you to make informed decisions, solve problems efficiently, and navigate the quantitative aspects of the world around you with confidence. By understanding the underlying concepts and employing various calculation methods, you can confidently tackle even the most challenging percentage-related problems.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 1.5 Percent Of 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.