What Is 1 Divided By 2/3
News Co
Apr 16, 2025 · 5 min read
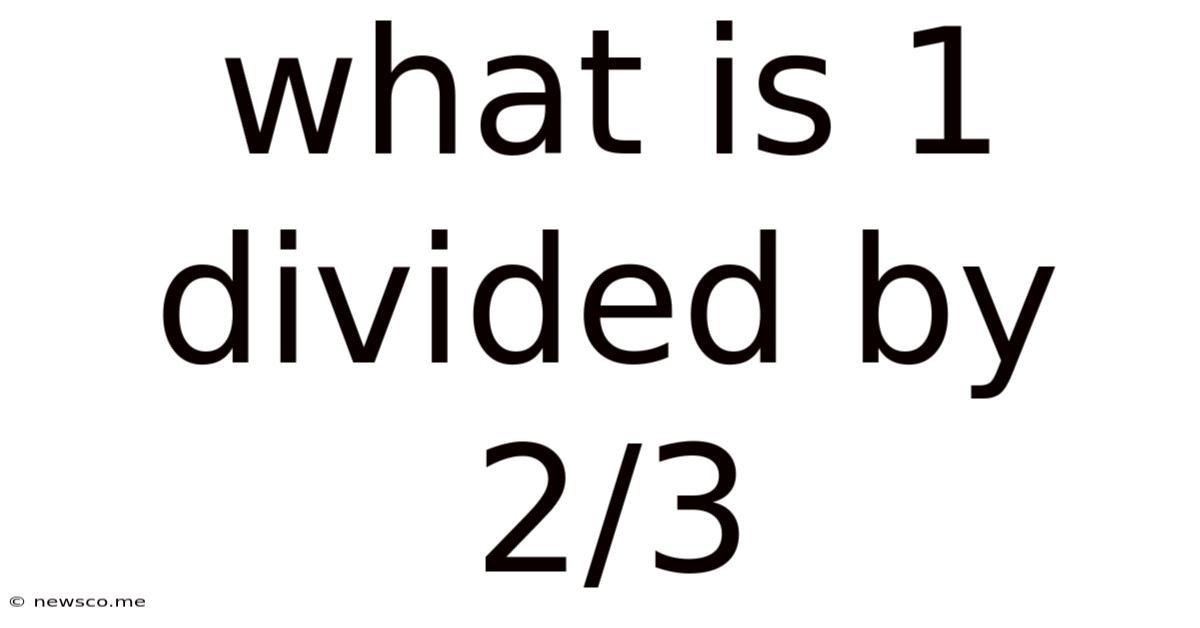
Table of Contents
What is 1 Divided by 2/3? A Deep Dive into Fraction Division
This seemingly simple question, "What is 1 divided by 2/3?", opens the door to a fascinating exploration of fraction division, a fundamental concept in mathematics with widespread applications in various fields. This comprehensive guide will not only provide the answer but also delve into the underlying principles, explore different methods of solving the problem, and demonstrate its practical relevance.
Understanding Fraction Division
Before tackling the specific problem, let's solidify our understanding of dividing fractions. Dividing by a fraction is essentially the same as multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 2/3 is 3/2.
This principle stems from the definition of division: division is the inverse operation of multiplication. If we divide a number 'a' by a number 'b', we are essentially asking, "What number, when multiplied by 'b', gives us 'a'?" Applying this to fractions leads to the reciprocal method.
Solving 1 Divided by 2/3
Now, let's apply this knowledge to our problem: 1 ÷ (2/3).
Following the rule of fraction division, we replace the division operation with multiplication and use the reciprocal of 2/3:
1 ÷ (2/3) = 1 × (3/2)
Multiplying the numerators (the top numbers) and the denominators (the bottom numbers), we get:
1 × 3 = 3 1 × 2 = 2
Therefore, the answer is 3/2, or 1 ½.
Alternative Methods and Visualizations
While the reciprocal method is the most efficient, let's explore alternative approaches to understand the problem more deeply.
Using a Visual Representation
Imagine a whole pizza (representing the number 1). If we divide this pizza into thirds (represented by 1/3), we have three equal slices. The question "1 divided by 2/3" asks how many 2/3 slices we can get from this whole pizza.
Since each 2/3 slice consists of two thirds, we can clearly see that we can obtain one and a half (1 ½) slices of 2/3 from a whole pizza. This visual representation confirms our mathematical calculation.
Converting to Decimals
We can also solve this using decimal equivalents. 2/3 is approximately 0.667 (it's a recurring decimal). Therefore, the problem becomes:
1 ÷ 0.667 ≈ 1.5
This decimal approach provides an approximate answer, which is close enough for many practical situations, but it lacks the precision of the fraction method.
Practical Applications of Fraction Division
The concept of dividing fractions, and specifically understanding problems like "1 divided by 2/3," has far-reaching applications in various real-world scenarios.
Cooking and Baking
Recipes often involve fractional measurements. If a recipe calls for 2/3 of a cup of flour, and you want to halve the recipe, you'll need to divide 2/3 by 2. Similarly, increasing a recipe requires multiplying the fractional measurements, which is intrinsically linked to division.
Construction and Engineering
Precision is paramount in construction and engineering. Calculations involving fractions and their divisions are common in determining measurements, materials, and proportions. Dividing lengths or volumes expressed as fractions is a routine task.
Finance and Economics
Financial calculations often involve fractions, especially when dealing with percentages, ratios, and shares. Dividing fractions plays a crucial role in calculating proportions of investments, profits, or debts.
Sewing and Tailoring
Pattern making and sewing rely on precise measurements. Dividing fabric lengths or adjusting pattern pieces often involves fractional calculations.
Expanding on the Concept: Dividing by Fractions Greater Than 1
Let's extend our understanding to include cases where we divide by a fraction greater than 1. For example, consider the problem: 1 ÷ (5/2).
Again, we use the reciprocal method:
1 ÷ (5/2) = 1 × (2/5) = 2/5
In this case, the result (2/5) is less than 1 because we are dividing by a number larger than 1. This highlights that dividing by a fraction larger than 1 results in a smaller value than the original number.
Advanced Concepts and Extensions
The principles discussed here form the foundation for more complex mathematical concepts. Understanding fraction division is crucial for mastering:
- Algebra: Solving algebraic equations often involves manipulating fractions and employing the rules of fraction division.
- Calculus: Derivatives and integrals frequently involve manipulating fractional expressions, making a solid understanding of fraction division essential.
- Higher-level mathematics: Many advanced mathematical concepts build upon the foundational principles of fraction division.
Troubleshooting Common Mistakes
When working with fraction division, several common errors can occur. Let's address them:
- Forgetting the reciprocal: The most common mistake is forgetting to invert the second fraction before multiplying. Always remember to take the reciprocal of the divisor (the fraction you are dividing by).
- Incorrect multiplication: Careless multiplication of numerators and denominators can lead to inaccurate results. Double-check your calculations.
- Simplifying fractions: After multiplying, ensure you simplify the resulting fraction to its lowest terms. This makes the answer more concise and easier to understand.
Conclusion: Mastering Fraction Division
The seemingly simple question, "What is 1 divided by 2/3?", serves as a gateway to understanding a fundamental mathematical operation with widespread applications. By mastering the principles of fraction division, including the reciprocal method and alternative approaches, you equip yourself with a powerful tool for tackling various mathematical challenges across numerous fields. Remember to practice consistently, identify and avoid common mistakes, and appreciate the versatility of this essential concept. The more you practice, the more comfortable and proficient you will become with fraction division, enabling you to confidently approach more complex mathematical problems.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 1 Divided By 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.