What Is 1 To The 3rd Power
News Co
Apr 06, 2025 · 5 min read
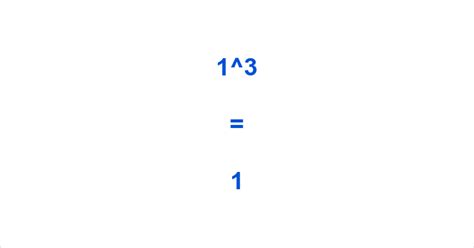
Table of Contents
What is 1 to the 3rd Power? A Deep Dive into Exponents and Their Applications
Understanding exponents is fundamental to grasping many concepts in mathematics, science, and even finance. This article delves into the seemingly simple question, "What is 1 to the 3rd power?" While the answer itself is straightforward, exploring the underlying principles provides a robust foundation for more complex calculations and applications.
Understanding Exponents: The Basics
Before we tackle 1 to the 3rd power, let's establish a solid understanding of exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. It's represented by a small number written slightly above and to the right of the base.
For example, in the expression 5³, 5 is the base, and 3 is the exponent. This means:
5³ = 5 x 5 x 5 = 125
The expression is read as "5 to the power of 3" or "5 cubed." The exponent 3 signifies that the base, 5, is multiplied by itself three times.
Calculating 1 to the 3rd Power
Now, let's address the question at hand: What is 1 to the 3rd power (1³)? Following the principle of exponents, this means:
1³ = 1 x 1 x 1 = 1
Therefore, 1 to the 3rd power equals 1. This holds true regardless of the exponent; any positive integer power of 1 will always equal 1.
Why Does 1 Raised to Any Power Equal 1?
The fact that 1 raised to any power equals 1 stems from the multiplicative identity property. The multiplicative identity is the number 1, which, when multiplied by any other number, leaves that number unchanged. In essence, multiplying by 1 doesn't alter the value.
Consequently, multiplying 1 by itself any number of times will always result in 1. This principle is crucial in various mathematical operations and simplifications.
Expanding the Concept: Negative Exponents and Zero Exponent
Our exploration shouldn't stop at positive integer exponents. Let's consider negative exponents and the zero exponent:
Negative Exponents
A negative exponent signifies the reciprocal of the base raised to the positive exponent. For instance:
x⁻ⁿ = 1/xⁿ
Applying this to the number 1:
1⁻³ = 1/1³ = 1/1 = 1
Again, we see that 1 raised to any negative power also equals 1. This consistent result highlights the unique properties of the number 1 within the realm of exponents.
Zero Exponent
Any non-zero number raised to the power of zero equals 1. This is a fundamental rule in algebra:
x⁰ = 1 (where x ≠ 0)
While the reasoning behind this might seem less intuitive than positive or negative exponents, it's crucial for maintaining consistency in mathematical operations and formulas. The exception, as noted, is that 0⁰ is undefined.
Real-World Applications of Exponents
The concept of exponents, seemingly simple in its basic form, has far-reaching applications in numerous fields:
Science
-
Compound Interest: In finance, compound interest calculations rely heavily on exponents. The formula A = P(1 + r/n)^(nt) uses exponents to determine the future value (A) of an investment based on the principal amount (P), interest rate (r), number of times interest is compounded per year (n), and the number of years (t).
-
Exponential Growth and Decay: Many natural phenomena, such as population growth, radioactive decay, and the spread of diseases, can be modeled using exponential functions. These functions utilize exponents to describe the rapid increase or decrease of a quantity over time.
-
Physics: Exponents are essential in various physics formulas, including those related to motion, gravity, and electromagnetism. For example, Newton's Law of Universal Gravitation uses exponents to describe the relationship between the gravitational force and the distance between two objects.
Computer Science
-
Binary Numbers: Computer systems operate on the binary system (base-2), which utilizes exponents of 2 to represent numbers. Understanding binary numbers and their representation requires a solid grasp of exponents.
-
Data Structures and Algorithms: Many data structures and algorithms' efficiency is expressed using Big O notation, which involves exponents to represent the growth rate of computational complexity as the input size increases.
Engineering
-
Structural Analysis: Engineers use exponents in formulas related to stress, strain, and material properties to ensure the stability and safety of structures.
-
Electrical Engineering: Exponential functions are crucial for understanding electrical circuits and the behavior of capacitors and inductors.
Economics and Finance
-
Present Value and Future Value Calculations: Exponents are critical in financial calculations related to present value and future value, enabling us to determine the worth of investments or debt over time.
-
Economic Growth Models: Exponents feature prominently in economic growth models that predict economic output based on factors like capital accumulation and technological progress.
Expanding on the Concept: Higher Powers of 1
While we focused on 1 to the 3rd power, let's briefly consider higher powers:
1⁴ = 1 x 1 x 1 x 1 = 1 1⁵ = 1 x 1 x 1 x 1 x 1 = 1 ...and so on.
The pattern is clear: regardless of how high the exponent, 1 raised to that power will always result in 1. This consistent behavior underscores the multiplicative identity property of 1 and its significance in various mathematical contexts.
Conclusion: The Significance of Simplicity
The seemingly trivial calculation of 1 to the 3rd power provides a gateway to understanding the fundamental principles of exponents. While the answer itself is straightforward, exploring the underlying concepts, including negative exponents, the zero exponent, and the multiplicative identity property, reveals the power and wide-ranging applications of this mathematical concept across diverse fields. Mastering exponents lays a solid foundation for tackling more complex mathematical problems and developing a deeper appreciation for the elegance and utility of mathematics in our world.
Latest Posts
Latest Posts
-
What Is Square Root Of 68
Apr 08, 2025
-
What Is 9 10 As A Percent
Apr 08, 2025
-
Can A Negative Number Be Rational
Apr 08, 2025
-
What Is The Measure Of Abc
Apr 08, 2025
-
Lcm Of 6 8 And 12
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 To The 3rd Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.