What Is 10/15 As A Percentage
News Co
Mar 22, 2025 · 4 min read
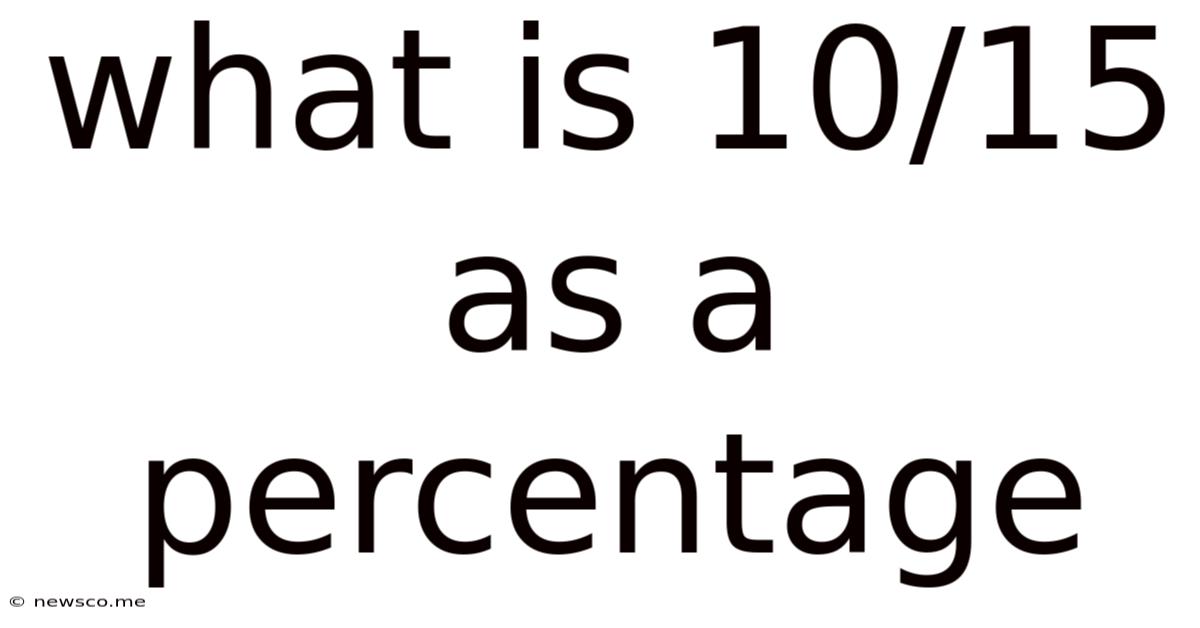
Table of Contents
What is 10/15 as a Percentage? A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with applications spanning various fields, from finance and statistics to everyday life. This comprehensive guide will delve into the process of converting the fraction 10/15 into a percentage, exploring the underlying principles, providing step-by-step instructions, and offering practical examples to solidify your understanding. We'll also touch upon related concepts and advanced applications.
Understanding Fractions and Percentages
Before diving into the conversion, let's establish a clear understanding of fractions and percentages.
Fractions: A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of parts the whole is divided into. In our case, 10/15 means we have 10 parts out of a total of 15 parts.
Percentages: A percentage represents a fraction of 100. The symbol "%" signifies "per hundred." Therefore, 50% means 50 out of 100, or 50/100. Percentages are often used to express proportions, rates, and changes.
Converting 10/15 to a Percentage: Step-by-Step
The conversion process involves two main steps:
Step 1: Simplify the Fraction (if possible)
The fraction 10/15 can be simplified by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD of 10 and 15 is 5. Dividing both the numerator and the denominator by 5, we get:
10 ÷ 5 = 2 15 ÷ 5 = 3
Therefore, the simplified fraction is 2/3. Simplifying the fraction makes the subsequent calculations easier.
Step 2: Convert the Simplified Fraction to a Percentage
To convert a fraction to a percentage, we multiply the fraction by 100%. This is equivalent to dividing the numerator by the denominator and then multiplying the result by 100.
(2/3) * 100% = (2 * 100) / 3 % = 200/3 %
Now, we perform the division:
200 ÷ 3 ≈ 66.67
Therefore, 10/15 is approximately equal to 66.67%.
Alternative Method: Decimal Conversion
Another approach involves first converting the fraction to a decimal and then converting the decimal to a percentage.
Step 1: Convert the Fraction to a Decimal
Divide the numerator by the denominator:
10 ÷ 15 ≈ 0.6667
Step 2: Convert the Decimal to a Percentage
Multiply the decimal by 100%:
0.6667 * 100% = 66.67%
This method yields the same result: 66.67%.
Practical Applications and Real-World Examples
The ability to convert fractions to percentages is crucial in numerous real-world scenarios:
- Calculating Grades: If you answered 10 out of 15 questions correctly on a test, your score is 66.67%.
- Financial Calculations: Understanding percentages is vital for calculating interest rates, discounts, and profit margins. For example, if a store offers a 10/15 discount on an item priced at $150, it means a discount of approximately 66.67%, resulting in a saving of about $100.
- Data Analysis: Percentages are frequently used to represent data in charts and graphs, facilitating easier comprehension of proportions and trends. A survey showing 10 out of 15 respondents prefer a particular product would be represented as a 66.67% preference rate.
- Sales and Marketing: Sales figures, conversion rates, and market share are often expressed as percentages to track performance and identify areas for improvement. For instance, if 10 out of 15 marketing campaigns are successful, the success rate is 66.67%.
Understanding Recurring Decimals
Notice that the decimal representation of 2/3 (0.6667) contains a repeating decimal (0.666...). This is because 2/3 is a rational number, but its decimal representation is non-terminating. In practical applications, we typically round the decimal to a certain number of decimal places for convenience. For example, we rounded 0.666... to 0.6667 in our calculations.
Advanced Applications: Percentage Change and Increase/Decrease
The concept of percentage extends to calculating percentage change, increase, or decrease. For example, if a quantity increases from 15 to 20, the percentage increase is calculated as:
[(20 - 15) / 15] * 100% = 33.33%
Similarly, if a quantity decreases from 20 to 15, the percentage decrease is calculated as:
[(20 - 15) / 20] * 100% = 25%
These calculations are essential for analyzing trends and comparing values over time.
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting fractions to percentages is a fundamental mathematical skill with broad practical applications. The process involves simplifying the fraction (if possible) and then multiplying the fraction by 100%. Alternatively, you can convert the fraction to a decimal first and then multiply by 100%. Understanding this process is crucial for tackling various problems in finance, statistics, data analysis, and other fields. Remember to round your answers appropriately depending on the context and desired level of precision. By mastering this skill, you'll enhance your mathematical proficiency and gain valuable insights from data presented in fractional and percentage forms. This comprehensive guide aims to equip you with the knowledge and confidence to handle such conversions effectively.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 10/15 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.