What Is 10/3 As A Mixed Number
News Co
Mar 22, 2025 · 5 min read
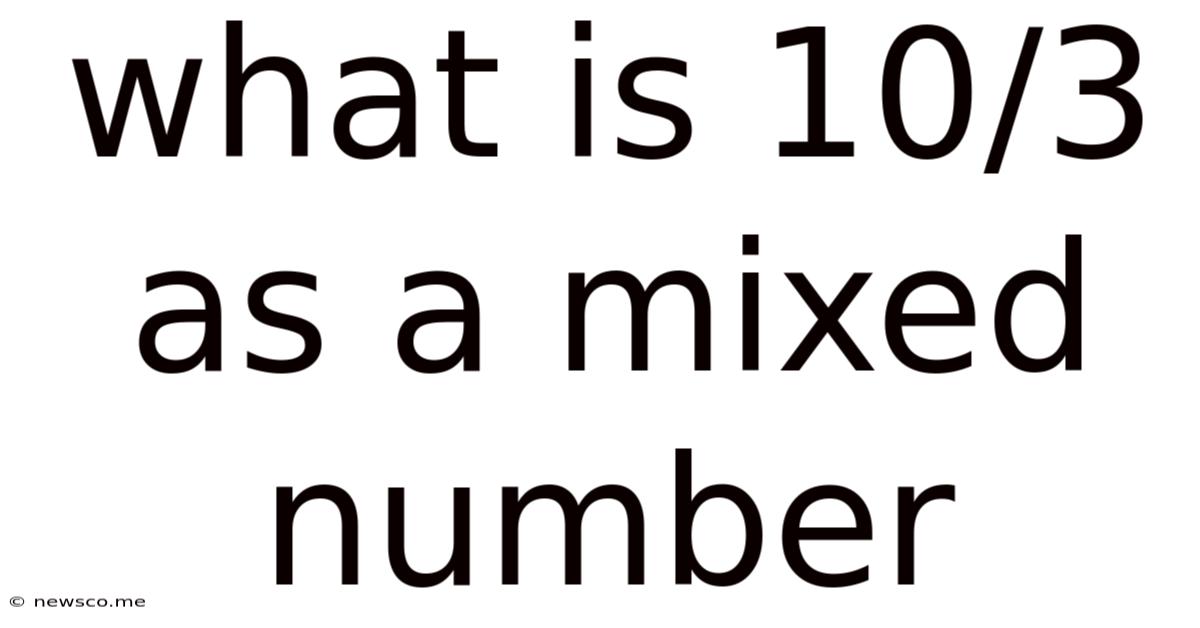
Table of Contents
What is 10/3 as a Mixed Number? A Comprehensive Guide
The seemingly simple question, "What is 10/3 as a mixed number?" opens a door to a fundamental concept in mathematics: understanding fractions and their representation. This comprehensive guide will not only answer this question but will also delve into the underlying principles, provide various methods for solving similar problems, and explore the practical applications of mixed numbers.
Understanding Fractions and Mixed Numbers
Before diving into the conversion, let's solidify our understanding of the core components. A fraction represents a part of a whole. It consists of two parts: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into.
A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator is smaller than the denominator (e.g., 1/2, 2/3, 3/4). Mixed numbers are useful for representing quantities that are greater than one but not a whole number. For example, 1 ½ represents one whole and one-half.
Converting 10/3 to a Mixed Number: Step-by-Step
The conversion of 10/3 to a mixed number involves dividing the numerator (10) by the denominator (3).
Step 1: Perform the Division
Divide 10 by 3: 10 ÷ 3 = 3 with a remainder of 1.
Step 2: Interpret the Result
- The quotient (3) becomes the whole number part of the mixed number.
- The remainder (1) becomes the numerator of the fractional part.
- The denominator remains the same (3).
Step 3: Write the Mixed Number
Therefore, 10/3 as a mixed number is 3 1/3.
Alternative Methods for Conversion
While the long division method is straightforward, other approaches can help solidify understanding and cater to different learning styles.
Method 2: Repeated Subtraction
This method involves repeatedly subtracting the denominator from the numerator until the result is less than the denominator.
- Start with the numerator (10).
- Subtract the denominator (3): 10 - 3 = 7
- Subtract the denominator again: 7 - 3 = 4
- Subtract the denominator again: 4 - 3 = 1
- We've subtracted the denominator three times (this is our whole number). The remaining 1 is our new numerator.
This leaves us with 3 and a remainder of 1, leading to the mixed number 3 1/3.
Method 3: Visual Representation
Visual aids are exceptionally helpful, especially for beginners. Imagine a group of 10 objects. We want to divide them into groups of 3.
- We can make three complete groups of 3.
- We have one object left over.
This visually demonstrates that we have 3 whole groups and 1/3 of another group, giving us 3 1/3.
Practical Applications of Mixed Numbers
Mixed numbers find extensive use in various real-world scenarios:
- Measurement: Imagine measuring the length of a piece of wood. It might be 3 and 1/3 feet long, neatly represented as a mixed number.
- Cooking: Recipes often use mixed numbers for ingredient quantities. For example, a recipe might call for 2 1/2 cups of flour.
- Construction: Building projects frequently involve measurements using mixed numbers for precision and clarity.
- Time: We regularly use mixed numbers to express time. For instance, 1 hour and 15 minutes can be written as 1 ¼ hours.
Converting Mixed Numbers to Improper Fractions
It's crucial to understand the reverse process – converting a mixed number back to an improper fraction. This is often necessary in calculations involving fractions.
To convert 3 1/3 to an improper fraction:
- Multiply the whole number (3) by the denominator (3): 3 x 3 = 9.
- Add the numerator (1) to the result: 9 + 1 = 10.
- Keep the same denominator (3).
This gives us the improper fraction 10/3, demonstrating the equivalence between the mixed number and the improper fraction.
Solving Problems Involving Mixed Numbers
Let's tackle a few example problems to solidify our understanding.
Example 1: What is 17/5 as a mixed number?
Following the steps:
- 17 ÷ 5 = 3 with a remainder of 2.
- The mixed number is 3 2/5.
Example 2: Add 2 1/4 and 1 3/4.
- Add the whole numbers: 2 + 1 = 3
- Add the fractions: 1/4 + 3/4 = 1
- Combine the results: 3 + 1 = 4
The answer is 4.
Example 3: Subtract 1 2/3 from 4 1/3.
- Subtract the whole numbers: 4 - 1 = 3
- Subtract the fractions: 1/3 - 2/3 = -1/3
- Since the fraction is negative, we borrow 1 from the whole number: 3 -1 = 2.
- Add the borrowed 1 (expressed as 3/3) to the fraction: 3/3 - 1/3 = 2/3
The answer is 2 2/3.
Conclusion: Mastering Mixed Numbers
Understanding the conversion between improper fractions and mixed numbers is fundamental to working comfortably with fractions in various contexts. By mastering this skill, you'll be better equipped to solve mathematical problems, interpret measurements, follow recipes, and engage with numerous real-world applications that rely on the precise representation of quantities. The various methods outlined here—long division, repeated subtraction, and visual representation—provide different avenues to grasp this important mathematical concept and choose the method that best suits your learning style. Remember to practice regularly to solidify your understanding and improve your efficiency in solving problems involving mixed numbers.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 10/3 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.