What Is 10 Percent Of 20
News Co
Mar 18, 2025 · 5 min read
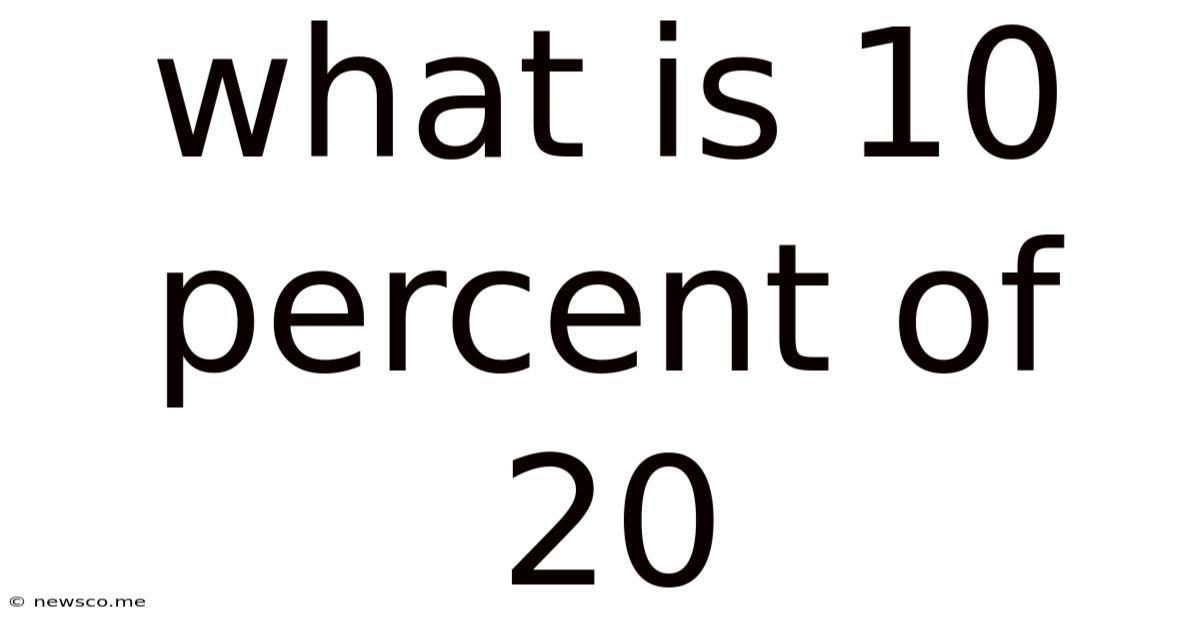
Table of Contents
What is 10 Percent of 20? A Deep Dive into Percentages and Their Applications
This seemingly simple question, "What is 10 percent of 20?", opens the door to a vast world of mathematical concepts and practical applications. While the answer itself is straightforward (2), understanding the underlying principles of percentages and how they're used in various fields is crucial for everyday life, financial literacy, and even advanced studies. This article will explore the calculation, delve into the significance of percentages, and showcase their relevance across numerous domains.
Calculating 10 Percent of 20: The Basics
The core of this problem lies in understanding the concept of percentage. A percentage is a fraction or ratio expressed as a number out of 100. Therefore, 10 percent can be written as 10/100 or 0.10. To find 10 percent of 20, we simply multiply 20 by 0.10:
20 x 0.10 = 2
Therefore, 10 percent of 20 is 2.
This simple calculation can be adapted to find any percentage of any number. The general formula is:
(Percentage/100) x Number = Result
Beyond the Calculation: Understanding Percentages in Context
While calculating 10 percent of 20 is elementary, the broader implications of percentage calculations are far-reaching. Percentages are essential tools for understanding and communicating proportions, ratios, and changes in values. Let's examine some common scenarios:
1. Financial Literacy: Discounts, Interest, and Taxes
Percentages are ubiquitous in finance. They're used to calculate:
- Discounts: A store offering a 20% discount on a $50 item will reduce the price by (20/100) x $50 = $10, resulting in a final price of $40.
- Interest: Banks and lending institutions use percentages to determine interest rates on loans and savings accounts. A 5% annual interest rate on a $1000 savings account means you'll earn (5/100) x $1000 = $50 in interest per year.
- Taxes: Sales tax, income tax, and other forms of taxation are expressed as percentages of the taxable amount. A 6% sales tax on a $25 purchase translates to (6/100) x $25 = $1.50 in tax.
Understanding percentage calculations is vital for making informed financial decisions, budgeting effectively, and managing personal finances.
2. Data Analysis and Statistics: Presenting Proportions and Trends
Percentages are crucial for interpreting data and presenting findings. They allow us to express proportions and changes in a clear and concise manner:
- Market Share: Companies use percentages to represent their market share within an industry. A company with a 15% market share holds 15 out of every 100 units sold in that particular market.
- Growth Rates: Economic growth, population growth, and business growth are often expressed as percentages to indicate the rate of change over time. A 3% annual growth rate suggests a 3% increase in value each year.
- Survey Results: Percentages are used extensively to summarize and present the results of surveys and polls. For example, "60% of respondents agreed with the statement..."
The ability to interpret and use percentages correctly is essential for making informed decisions based on data.
3. Science and Engineering: Precision and Measurement
In scientific and engineering fields, percentages often represent precision and error margins:
- Experimental Error: Scientists report experimental results with error margins expressed as percentages. This indicates the degree of uncertainty associated with the measurement.
- Material Composition: The composition of alloys and other materials is often specified in terms of percentages of different elements. For instance, a steel alloy might consist of 98% iron and 2% carbon.
- Efficiency Calculations: The efficiency of machines and processes is often expressed as a percentage. A machine with 85% efficiency means it converts 85% of the input energy into useful work.
Accuracy in percentage calculations is vital for maintaining precision and reliability in these domains.
Advanced Percentage Calculations: Beyond the Basics
While finding 10 percent of 20 is simple, more complex calculations involving percentages are frequently encountered:
1. Finding the Original Value: Reverse Percentage Calculations
Sometimes, you know the percentage increase or decrease and the final value, but need to determine the original value. For example:
-
Problem: After a 10% discount, a product costs $18. What was the original price?
-
Solution: The final price represents 90% (100% - 10%) of the original price. We can set up an equation:
0.90x = $18
x = $18 / 0.90 = $20
The original price was $20.
2. Calculating Percentage Change: Growth and Decline
Percentage change is used to compare two values over time or across different groups. The formula for percentage change is:
[(New Value - Old Value) / Old Value] x 100%
For example, if sales increased from $1000 to $1200, the percentage increase is:
[(1200 - 1000) / 1000] x 100% = 20%
3. Compounding Percentages: Interest and Growth
Compounding percentages occur when a percentage is applied to a value, and then that new value is used for subsequent calculations. This is commonly seen with compound interest:
- Example: If you invest $1000 at a 5% annual compound interest rate, after one year you will have $1050. In the second year, the 5% interest is applied to $1050, not $1000, leading to a higher final value.
Understanding compound interest is crucial for long-term financial planning and investment strategies.
The Practical Applications of Percentages: Real-World Examples
Let's consider some real-world scenarios where understanding percentages is indispensable:
- Shopping: Calculating discounts, sales tax, and comparing prices.
- Investing: Understanding interest rates, returns, and risk.
- Cooking: Scaling recipes up or down based on percentages.
- Data Analysis: Interpreting statistics and trends in reports and articles.
- Real Estate: Calculating property taxes, mortgage interest, and appreciation.
- Health and Fitness: Tracking progress towards fitness goals, calculating body fat percentage, and interpreting health data.
Conclusion: Mastering Percentages for a Better Understanding of the World
While "What is 10 percent of 20?" may seem trivial at first glance, it opens up a world of mathematical and practical applications. A thorough understanding of percentages is essential for navigating everyday life, making informed financial decisions, interpreting data, and succeeding in various professional fields. By mastering these fundamental calculations and their variations, we enhance our ability to comprehend and interact with the numerical aspects of the world around us. The simple act of calculating 10% of 20 serves as a gateway to a much broader and significant understanding of the role of percentages in our daily lives. Remember that consistent practice and application are key to solidifying your understanding and becoming proficient in percentage calculations.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 Percent Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.