What Is 10 Percent Of 60
News Co
Mar 20, 2025 · 5 min read
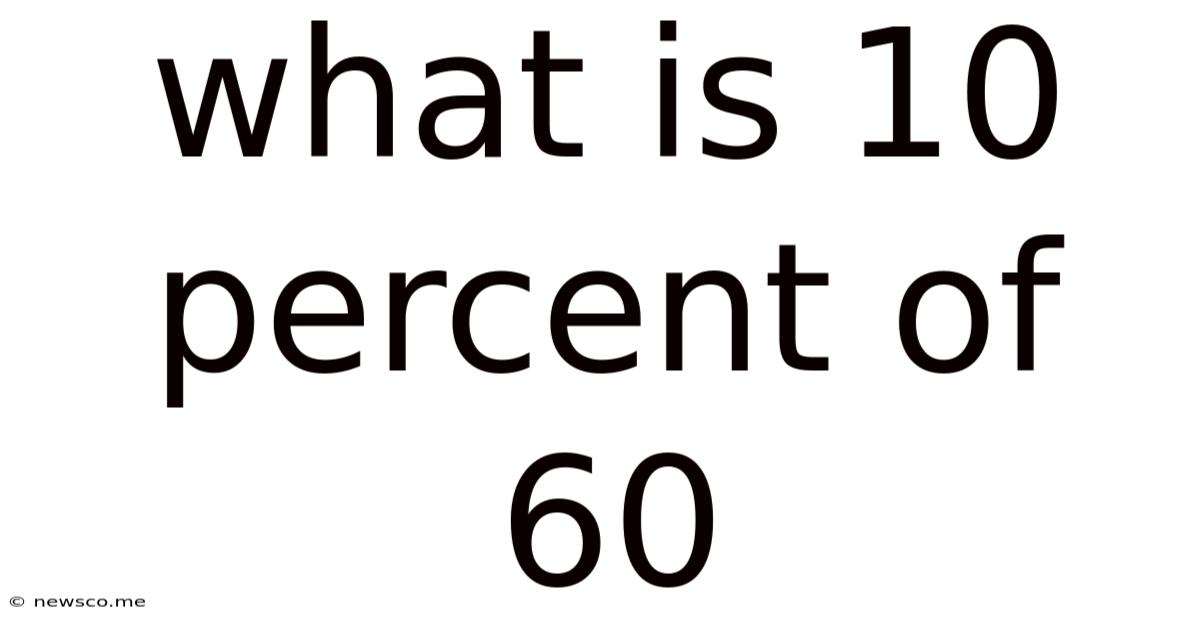
Table of Contents
What is 10 Percent of 60? A Deep Dive into Percentages and Their Applications
This seemingly simple question, "What is 10 percent of 60?", opens the door to a vast world of mathematical concepts and practical applications. While the answer itself is straightforward (6), understanding the underlying principles of percentages and how they are calculated provides a powerful tool for various situations in everyday life, business, and beyond. This article will not only answer the initial question but also explore the broader context of percentage calculations, offering examples and demonstrating their relevance.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred." So, 10 percent (written as 10%) means 10 out of every 100. This representation allows for easy comparison of proportions across different quantities.
The Formula for Calculating Percentages
The fundamental formula for calculating a percentage of a number is:
(Percentage/100) * Number = Result
In our example, "What is 10 percent of 60?", we plug in the values:
(10/100) * 60 = 6
Therefore, 10 percent of 60 is 6.
Beyond the Basics: Different Methods for Calculating Percentages
While the standard formula is efficient, there are alternative methods that can be helpful depending on the context and your comfort level with numbers.
Method 1: Using Decimal Equivalents
Percentages can be easily converted to decimal equivalents by dividing the percentage by 100. In our case, 10% becomes 0.10. The calculation then simplifies to:
0.10 * 60 = 6
This method is often faster, especially when working with more complex calculations or using a calculator.
Method 2: Finding 1% and Scaling Up
Another approach involves finding 1% of the number first and then multiplying to get the desired percentage. 1% of 60 is:
(1/100) * 60 = 0.6
To find 10%, we simply multiply this result by 10:
0.6 * 10 = 6
This method is particularly useful when dealing with mental calculations or percentages that are multiples of 1%.
Method 3: Using Proportions
Percentages can also be solved using proportions. We can set up a proportion where 'x' represents the unknown value:
10/100 = x/60
Cross-multiplying and solving for 'x' gives us:
100x = 600
x = 6
This method emphasizes the proportional relationship between the percentage and the whole number.
Practical Applications of Percentage Calculations
The ability to calculate percentages is essential in numerous real-world scenarios. Here are just a few examples:
1. Sales and Discounts
Retail stores frequently advertise discounts as percentages. Understanding percentages allows you to quickly calculate the final price of an item after a discount is applied. For example, a 20% discount on a $50 item means a saving of:
(20/100) * $50 = $10
The final price would be $50 - $10 = $40.
2. Taxes and Tips
Calculating taxes and service tips often involves percentage calculations. For instance, if the sales tax is 6%, and your meal cost $75, the tax amount would be:
(6/100) * $75 = $4.50
The total bill would be $75 + $4.50 = $79.50. Similarly, calculating a 15% tip on the meal is straightforward using the percentage formula.
3. Financial Calculations
Percentages are crucial in financial planning and management. Understanding interest rates, return on investment (ROI), and growth rates all depend on accurately calculating percentages. For example, calculating compound interest involves repeated percentage calculations over time.
4. Data Analysis and Statistics
Percentages are fundamental in presenting and interpreting data. Statistics frequently involve expressing data as percentages to provide a clear and concise understanding of proportions and trends. For example, survey results often show percentages to represent the proportion of respondents who chose a particular option.
5. Everyday Life Scenarios
Beyond formal settings, percentages are used daily in various contexts:
- Recipe adjustments: Scaling recipes up or down often requires adjusting ingredient quantities using percentages.
- Comparing prices: Determining which product offers better value for money requires comparing prices and using percentages to calculate unit costs.
- Understanding progress: Tracking progress towards a goal, such as completing a project or saving a certain amount of money, often involves measuring progress as a percentage.
Advanced Percentage Calculations: Beyond the Basics
While simple percentage calculations are relatively straightforward, more complex scenarios require a deeper understanding of mathematical principles:
1. Calculating Percentage Increase or Decrease
This involves calculating the change in a value relative to its initial value. The formula is:
[(New Value - Old Value) / Old Value] * 100%
For example, if the price of an item increases from $50 to $60, the percentage increase is:
[(60 - 50) / 50] * 100% = 20%
2. Finding the Original Value after a Percentage Change
If you know the final value after a percentage increase or decrease, you can work backward to find the original value. This often involves using algebraic equations and manipulation.
3. Working with Multiple Percentages
Calculating consecutive percentage changes, such as discounts applied one after another, requires careful consideration of the order of operations. It is essential to apply the percentages sequentially, rather than summing them directly.
Tools and Resources for Percentage Calculations
While mental math and basic calculations are sufficient for many percentage problems, several tools can assist with more complex calculations:
- Calculators: Standard calculators have percentage functions that simplify calculations.
- Spreadsheet software (like Excel or Google Sheets): Spreadsheets offer powerful functions for percentage calculations, allowing for batch processing and complex formula implementation.
- Online Percentage Calculators: Numerous online calculators are readily available for performing various percentage calculations. However, understanding the underlying principles remains vital for proper use and interpretation.
Conclusion: Mastering Percentages for a More Numerate Life
Understanding percentages is not just about solving mathematical problems; it’s a fundamental skill that empowers you to navigate the quantitative aspects of daily life more effectively. From financial decisions to data analysis, the ability to confidently calculate and interpret percentages provides a significant advantage in various contexts. This article has explored the basics and beyond, providing a comprehensive guide to mastering percentage calculations and applying them to real-world scenarios. Remember to practice regularly and explore different methods to solidify your understanding and build your confidence in this essential mathematical skill. The seemingly simple question, "What is 10 percent of 60?", serves as a springboard to a deeper appreciation of the pervasive role of percentages in our world.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 Percent Of 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.