What Is 10 To The Negative 2nd Power
News Co
Apr 17, 2025 · 5 min read
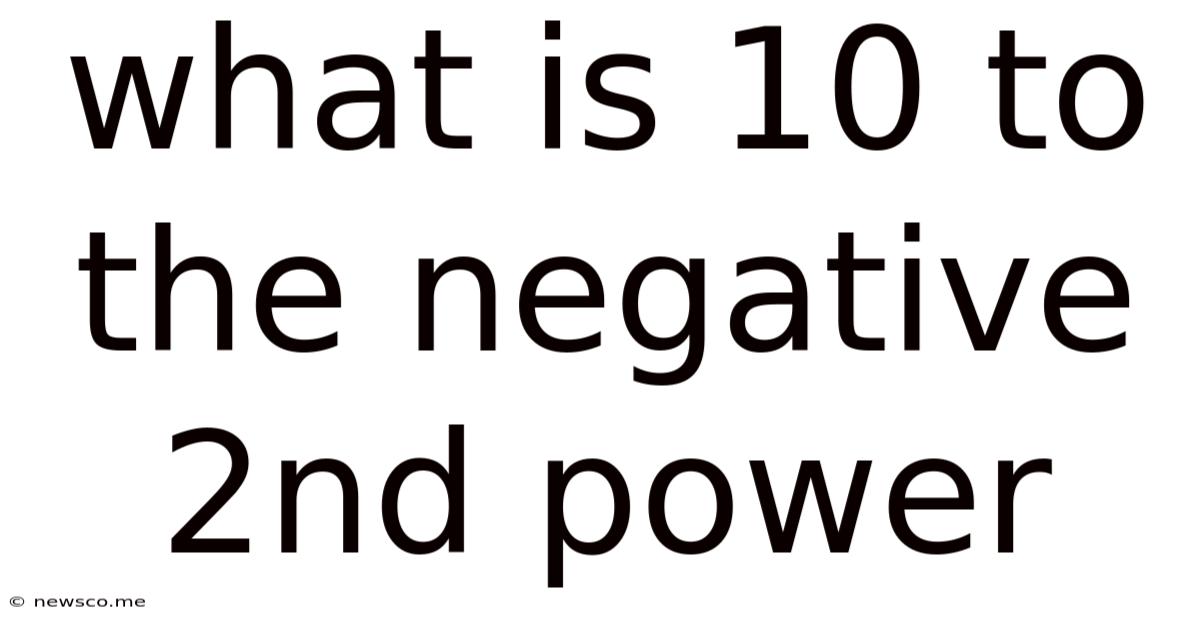
Table of Contents
What is 10 to the Negative 2nd Power? A Comprehensive Guide
Understanding exponents, especially negative ones, can sometimes feel daunting. But fear not! This comprehensive guide will demystify the concept of "10 to the negative 2nd power," explaining not only what it means but also its practical applications and broader implications within mathematics and science.
Deciphering the Notation: 10<sup>-2</sup>
The expression "10 to the negative 2nd power," often written as 10<sup>-2</sup>, represents a specific mathematical operation. It signifies the reciprocal of 10 raised to the positive second power (10²). Let's break this down:
-
10² (10 to the power of 2): This is simply 10 multiplied by itself: 10 x 10 = 100. This is a straightforward example of positive exponents.
-
Reciprocal: The reciprocal of a number is simply 1 divided by that number. For example, the reciprocal of 5 is 1/5, and the reciprocal of 100 is 1/100.
Therefore, 10<sup>-2</sup> is the reciprocal of 10², which is 1/100.
In simpler terms: 10<sup>-2</sup> = 1/100 = 0.01
Understanding Negative Exponents
Negative exponents are a crucial concept in mathematics. They are a concise way of expressing fractions and reciprocals. The general rule is:
a<sup>-n</sup> = 1/a<sup>n</sup>
Where 'a' is any non-zero number and 'n' is the exponent. This rule applies to all bases, not just 10. For example:
- 2<sup>-3</sup> = 1/2³ = 1/8 = 0.125
- 5<sup>-1</sup> = 1/5¹ = 1/5 = 0.2
The Significance of 10<sup>-2</sup> in Scientific Notation
Scientific notation is a powerful tool used to represent extremely large or extremely small numbers in a compact and manageable format. It's particularly prevalent in science and engineering. The core of scientific notation is expressing a number as a product of a number between 1 and 10, and a power of 10.
10<sup>-2</sup> plays a vital role in this system because it represents a shift of the decimal point two places to the left. Consider the number 0.01. In scientific notation, this is written as 1 x 10<sup>-2</sup>. We've moved the decimal point two places to the right to get the number 1 (a number between 1 and 10), and the negative exponent (-2) indicates the number of places we shifted the decimal point.
Practical Applications of 10<sup>-2</sup>
The value 10<sup>-2</sup> (or 0.01) appears frequently in various contexts:
1. Metric System: Centimeters and Square Centimeters
The metric system relies heavily on powers of 10. The prefix "centi" means one-hundredth. Therefore:
- 1 centimeter (cm) = 10<sup>-2</sup> meters (m) There are 100 centimeters in a meter.
- 1 square centimeter (cm²) = 10<sup>-4</sup> square meters (m²) This is because area is calculated by multiplying two lengths, so (10<sup>-2</sup> m) x (10<sup>-2</sup> m) = 10<sup>-4</sup> m²
2. Percentage Calculations
Percentages are essentially fractions expressed as parts of 100. 1% is equal to 1/100, which is the same as 10<sup>-2</sup>. For example, 5% can be written as 0.05 or 5 x 10<sup>-2</sup>.
3. Financial Calculations: Interest Rates and Compound Interest
Interest rates are often expressed as percentages. Understanding powers of 10, including 10<sup>-2</sup>, is essential when calculating compound interest over multiple periods.
4. Scientific Measurements: Units and Conversions
Many scientific measurements involve very small quantities, expressed using prefixes such as milli-, micro-, and nano-. These prefixes are directly related to powers of 10, and understanding 10<sup>-2</sup> forms a foundational step in grasping these smaller units.
5. Computer Science: Data Representation and Binary Systems
While not directly involving base 10, understanding negative exponents is vital in binary systems and data representation in computer science, where powers of 2 (and their reciprocals) are crucial.
Expanding on the Concept: Powers of 10 and Scientific Notation
It's essential to grasp the broader context of 10<sup>-2</sup> within the framework of powers of 10. Here's a quick overview:
- 10<sup>0</sup> = 1: Any number to the power of 0 is 1.
- 10<sup>1</sup> = 10: The base number itself.
- 10<sup>2</sup> = 100: The base number multiplied by itself.
- 10<sup>3</sup> = 1000: The base number multiplied by itself three times.
- 10<sup>-1</sup> = 0.1: One tenth.
- 10<sup>-2</sup> = 0.01: One hundredth.
- 10<sup>-3</sup> = 0.001: One thousandth.
Notice the pattern: As the exponent increases, the value increases. As the exponent decreases (becomes more negative), the value decreases (becomes a smaller fraction).
Beyond the Basics: Working with Negative Exponents
Here are some rules and examples to further solidify your understanding of negative exponents:
-
Multiplication of powers with the same base: a<sup>m</sup> x a<sup>n</sup> = a<sup>m+n</sup>. This applies even when exponents are negative. For example: 10<sup>-2</sup> x 10<sup>3</sup> = 10<sup>1</sup> = 10.
-
Division of powers with the same base: a<sup>m</sup> / a<sup>n</sup> = a<sup>m-n</sup>. Again, this rule holds true for negative exponents. For example: 10<sup>-2</sup> / 10<sup>-4</sup> = 10<sup>2</sup> = 100.
-
Power of a power: (a<sup>m</sup>)<sup>n</sup> = a<sup>m x n</sup>. This rule applies to negative exponents as well. For example: (10<sup>-2</sup>)<sup>3</sup> = 10<sup>-6</sup> = 0.000001.
Conclusion: Mastering 10<sup>-2</sup> and its Implications
Understanding "10 to the negative 2nd power" is not merely about memorizing a numerical value (0.01). It’s about grasping the underlying principles of exponents, reciprocals, and their application in scientific notation, various measurement systems, and more. This concept forms a cornerstone for advanced mathematical operations, and its applications extend across numerous fields, from scientific research to financial modeling. By thoroughly grasping this seemingly simple concept, you unlock a deeper understanding of the mathematical language used to describe our world. The ability to confidently work with negative exponents is a key skill for success in many scientific and technical endeavors.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 10 To The Negative 2nd Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.