What Is 10 To The Negative 4th Power
News Co
Apr 20, 2025 · 5 min read
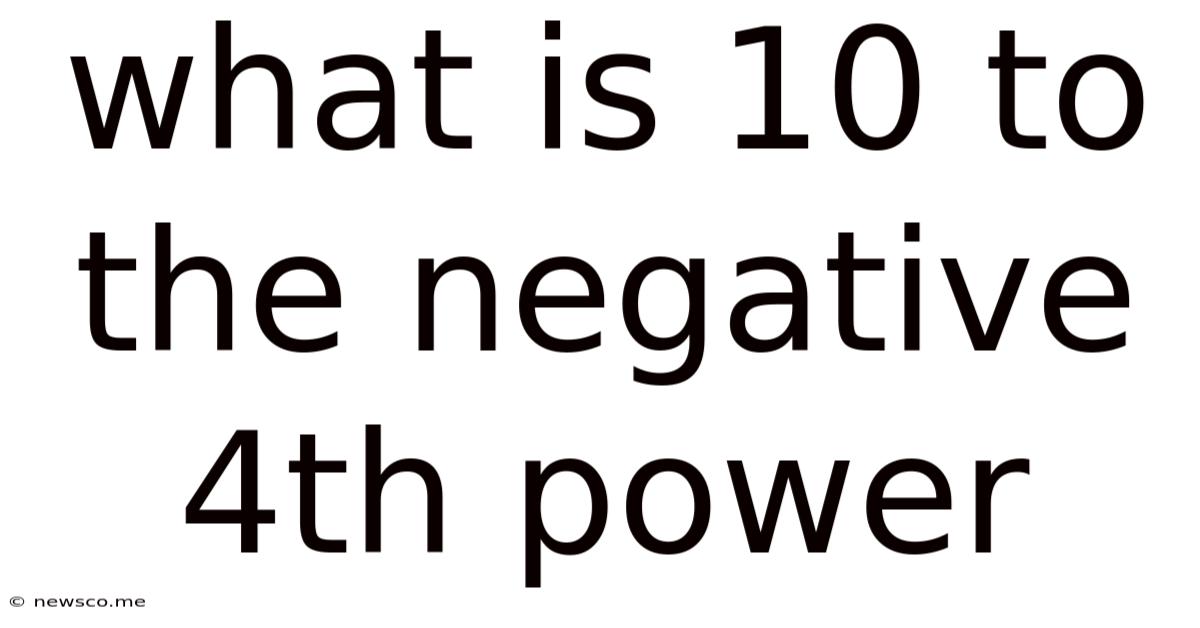
Table of Contents
What is 10 to the Negative 4th Power? A Deep Dive into Scientific Notation
Understanding scientific notation is crucial for anyone working with very large or very small numbers, common in fields like science, engineering, and finance. This article delves deep into the meaning of 10 to the negative 4th power (10⁻⁴), explaining its value, applications, and how it relates to other concepts in mathematics and science. We’ll explore the underlying principles, provide practical examples, and equip you with the knowledge to confidently handle similar exponential expressions.
Understanding Exponents and Negative Exponents
Before tackling 10⁻⁴, let's review the fundamentals of exponents. An exponent (or power) indicates how many times a base number is multiplied by itself. For example:
- 10² = 10 × 10 = 100 (10 to the power of 2, or 10 squared)
- 10³ = 10 × 10 × 10 = 1000 (10 to the power of 3, or 10 cubed)
Negative exponents represent the reciprocal of the positive exponent. In simpler terms, they indicate division rather than multiplication. The rule is:
a⁻ⁿ = 1/aⁿ
Therefore, 10⁻⁴ means the reciprocal of 10⁴.
Calculating 10 to the Negative 4th Power
Applying the rule for negative exponents:
10⁻⁴ = 1/10⁴
Now, let's calculate 10⁴:
10⁴ = 10 × 10 × 10 × 10 = 10,000
Substituting this back into the equation:
10⁻⁴ = 1/10,000 = 0.0001
Therefore, 10 to the negative 4th power is equal to 0.0001.
Significance of 10 to the Negative 4th Power in Scientific Notation
Scientific notation is a standardized way to represent very large or very small numbers using powers of 10. It significantly simplifies calculations and improves readability. Numbers are written in the form:
a x 10ᵇ
where 'a' is a number between 1 and 10 (but not including 10), and 'b' is an integer exponent.
10⁻⁴, expressed as 1 x 10⁻⁴, is a prime example of a number easily represented and manipulated using scientific notation. Its compact form highlights its magnitude much more clearly than the decimal equivalent, 0.0001.
Real-World Applications of 10 to the Negative 4th Power
The value 0.0001, or 10⁻⁴, appears frequently in various scientific and engineering contexts:
1. Micrometers (µm): Units of Measurement
Micrometers, often used to measure incredibly small lengths, are directly related to 10⁻⁴. One micrometer is equal to 10⁻⁶ meters. Consequently, 0.0001 meters (or 10⁻⁴ meters) is equivalent to 100 micrometers (100 µm). This conversion is crucial in microscopy, nanotechnology, and materials science.
2. Electrical Engineering: Resistance and Capacitance
In electronics, you may encounter resistances or capacitances expressed in scientific notation with negative exponents. These tiny values reflect the intricate workings of microchips and electronic circuits. For instance, a capacitor might have a capacitance of 1 x 10⁻⁴ Farads, indicating its small ability to store charge.
3. Chemistry: Molarity and Concentrations
In chemistry, expressing concentrations often requires using scientific notation. Imagine a solution with a molarity of 1 x 10⁻⁴ M (moles per liter). This extremely dilute concentration demonstrates the precision required in certain chemical analyses.
4. Physics: Wave Phenomena
10⁻⁴ might represent a small wavelength or amplitude in wave phenomena studies, such as sound or light. This precision is essential for understanding and describing various wave behaviours.
5. Finance: Interest Rates and Fractional Changes
While less common than in the sciences, financial modelling may involve extremely small changes, sometimes represented using powers of 10. Consider a small percentage change (0.01%) in the value of an asset; this change can be expressed using scientific notation involving a negative exponent.
Expanding on Exponents and Scientific Notation
To further solidify your understanding, let's explore some related concepts:
1. Powers of 10: The Foundation of Scientific Notation
Powers of 10 are fundamental to scientific notation. Understanding how they work is key to mastering the system. Consider the following:
- 10⁰ = 1
- 10¹ = 10
- 10² = 100
- 10³ = 1000
- 10⁻¹ = 0.1
- 10⁻² = 0.01
- 10⁻³ = 0.001
- 10⁻⁴ = 0.0001
Each increase in the exponent by 1 represents multiplication by 10, while each decrease represents division by 10.
2. Converting between Decimal and Scientific Notation
Converting between decimal and scientific notation is a valuable skill. To convert a decimal number to scientific notation, move the decimal point until you have a number between 1 and 10. The number of places you moved the decimal point becomes the exponent. If you moved it to the left, the exponent is positive; if to the right, it's negative.
3. Performing Calculations with Scientific Notation
Adding, subtracting, multiplying, and dividing numbers in scientific notation requires understanding how exponents work. When multiplying, you add the exponents; when dividing, you subtract them. Adding and subtracting requires adjusting the exponents to have the same power of 10 before combining the coefficients.
Practical Exercises
To reinforce your understanding, try the following exercises:
-
Convert the following decimal numbers to scientific notation:
- 0.00005
- 35000000
- 0.000000082
-
Convert the following numbers from scientific notation to decimal form:
- 2.5 x 10⁵
- 7.1 x 10⁻³
- 9 x 10⁻⁶
-
Perform the following calculations:
- (2 x 10³) x (4 x 10⁻²)
- (6 x 10⁻⁵) / (3 x 10⁻²)
- (5 x 10²) + (2 x 10¹)
Conclusion: Mastering 10 to the Negative 4th Power and Beyond
Understanding 10 to the negative 4th power—its meaning (0.0001), its representation in scientific notation (1 x 10⁻⁴), and its applications in various scientific and engineering disciplines—is fundamental to working comfortably with extremely small values. This knowledge, coupled with a grasp of exponents and scientific notation, empowers you to handle calculations involving these numbers effectively. By mastering these concepts, you'll find yourself better equipped to navigate the world of scientific and numerical analysis with confidence and precision. Remember to practice regularly to solidify your understanding and expand your capabilities in working with these vital mathematical tools.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 10 To The Negative 4th Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.