What Is 10 To The Power Of 2
News Co
Mar 17, 2025 · 5 min read
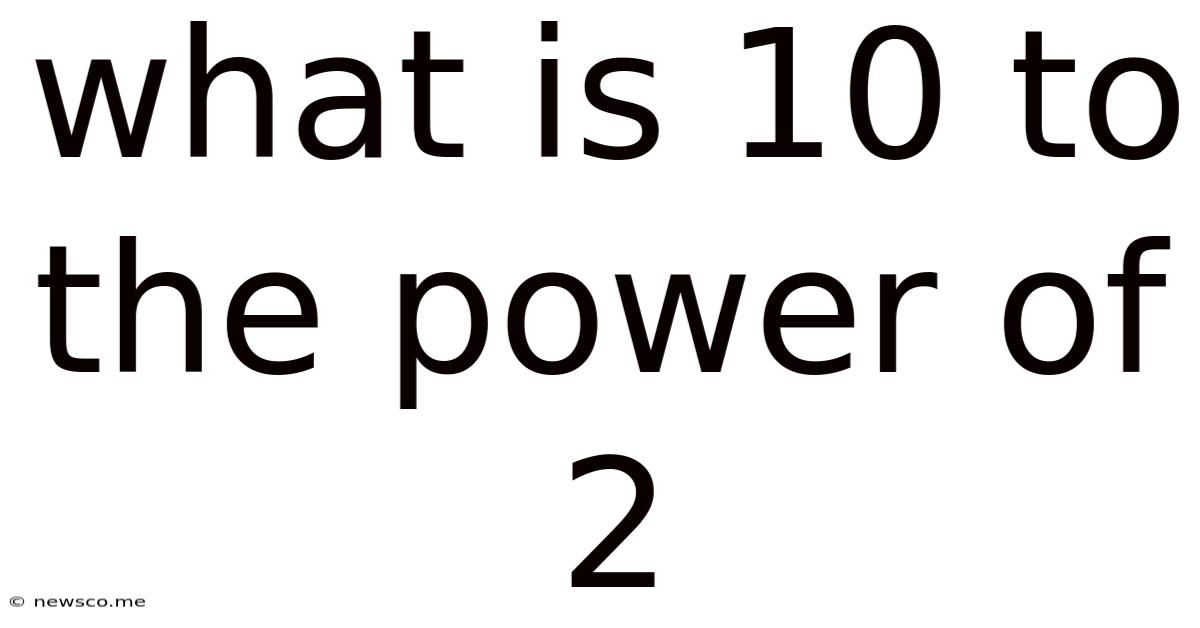
Table of Contents
What is 10 to the Power of 2? A Deep Dive into Exponents and Their Applications
The seemingly simple question, "What is 10 to the power of 2?" opens a door to a vast world of mathematics, encompassing exponents, their properties, and their widespread applications across various fields. This article will not only answer the initial question but delve into the broader context of exponents, exploring their meaning, how to calculate them, and their significance in diverse areas like science, finance, and computer science.
Understanding Exponents: The Basics
Before we tackle 10 to the power of 2, let's establish a firm grasp of exponents. An exponent, also known as a power or index, indicates how many times a base number is multiplied by itself. It's written as a superscript above the base number. For example, in the expression 10², the '2' is the exponent, and the '10' is the base. This is read as "10 raised to the power of 2" or "10 squared."
The Fundamental Formula:
The general representation of an exponent is: bⁿ, where 'b' is the base and 'n' is the exponent. This means 'b' is multiplied by itself 'n' times.
Examples:
- 2³ = 2 * 2 * 2 = 8 (2 cubed or 2 to the power of 3)
- 5¹ = 5 (Any number raised to the power of 1 is itself)
- 7⁰ = 1 (Any non-zero number raised to the power of 0 is 1)
- 4⁻² = 1/(4²) = 1/16 (Negative exponents represent reciprocals)
Calculating 10 to the Power of 2
Now, let's address the central question: What is 10 to the power of 2 (10²)?
Simply put, 10² means 10 multiplied by itself twice: 10 * 10 = 100.
Therefore, 10 to the power of 2 is equal to 100.
This seemingly straightforward calculation forms the foundation for understanding more complex exponential operations and their practical applications.
Beyond the Basics: Properties of Exponents
Understanding the fundamental properties of exponents is crucial for efficient calculation and problem-solving. These properties allow us to simplify complex expressions and manipulate equations effectively. Key properties include:
-
Product of Powers: When multiplying two numbers with the same base, add their exponents: bᵐ * bⁿ = bᵐ⁺ⁿ. For example, 2³ * 2² = 2⁵ = 32.
-
Quotient of Powers: When dividing two numbers with the same base, subtract their exponents: bᵐ / bⁿ = bᵐ⁻ⁿ. For example, 3⁵ / 3² = 3³ = 27.
-
Power of a Power: When raising a power to another power, multiply the exponents: (bᵐ)ⁿ = bᵐⁿ. For example, (2²)³ = 2⁶ = 64.
-
Power of a Product: When raising a product to a power, raise each factor to that power: (ab)ⁿ = aⁿbⁿ. For example, (2*3)² = 2² * 3² = 4 * 9 = 36.
-
Power of a Quotient: When raising a quotient to a power, raise both the numerator and the denominator to that power: (a/b)ⁿ = aⁿ/bⁿ. For example, (2/3)² = 2²/3² = 4/9.
The Significance of 10 to the Power of 2 and its Applications
While 10² = 100 might seem like a simple calculation, its significance extends far beyond basic arithmetic. Understanding this fundamental concept opens doors to numerous applications:
1. Metric System:
The metric system, the most widely used system of measurement globally, is fundamentally based on powers of 10. Understanding 10² helps us understand units like:
- Area: 100 square centimeters (cm²) is equivalent to 1 square decimeter (dm²) (10 cm x 10 cm).
- Volume: Understanding 10² helps in calculating cubic units when working with 3D spaces.
2. Scientific Notation:
Scientific notation is essential for representing extremely large or small numbers in a concise and manageable format. It often employs powers of 10. For example, the speed of light, approximately 300,000,000 meters per second, is expressed in scientific notation as 3 x 10⁸ m/s. Understanding 10² lays the groundwork for grasping the magnitude of these numbers.
3. Financial Calculations:
Compound interest, a cornerstone of financial planning, relies heavily on exponential growth. Calculating compound interest often involves raising numbers to powers, and understanding the fundamental concept of 10² provides a solid foundation for these calculations.
4. Computer Science and Data Storage:
In computer science, powers of 10 (and powers of 2) are frequently used in representing data sizes. Kilobytes (KB), Megabytes (MB), Gigabytes (GB), and Terabytes (TB) are all multiples of bytes, with the prefixes indicating powers of 10 (or 2, in some contexts). Understanding exponents enables us to convert between these units. For example, 1 MB is 1024 KB, a power of 2 used in computer memory.
5. Geometry and Area Calculations:
Calculating the area of squares and other geometric shapes frequently involves squaring values (raising to the power of 2). The area of a square with a side length of 10 units is 10² = 100 square units.
6. Physics and Engineering:
Many physical laws and engineering principles involve exponential relationships. For example, the intensity of light decreases proportionally to the square of the distance from the source. This is often represented by formulas employing powers of 10.
Expanding Your Knowledge: Exponents Beyond 2
While this article focuses on 10², it's crucial to understand that exponents can be any real number, not just positive integers. This opens up even more mathematical possibilities. For instance:
-
Fractional Exponents: These represent roots. For example, 10^(1/2) is the square root of 10, and 10^(1/3) is the cube root of 10.
-
Decimal Exponents: These represent intermediate values between integers. For example, 10².⁵ represents a value between 10² and 10³.
-
Negative Exponents: As mentioned earlier, these represent reciprocals. For example, 10⁻¹ = 1/10 = 0.1.
Conclusion: The Power of Understanding Exponents
The seemingly simple question, "What is 10 to the power of 2?" unravels into a rich understanding of exponents and their wide-ranging applications. From fundamental arithmetic to complex scientific calculations, mastering exponents is essential for success in numerous fields. This article provided a solid foundation for understanding exponents, their properties, and their significance across various disciplines. As you continue your mathematical journey, remember that the power of understanding exponents extends far beyond simple calculations; it's a fundamental building block for problem-solving and innovation. Through a strong grasp of these principles, you'll be better equipped to tackle challenges and explore the exciting world of mathematics and its applications.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 To The Power Of 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.