What Is 12 To The Power Of 3
News Co
Apr 26, 2025 · 5 min read
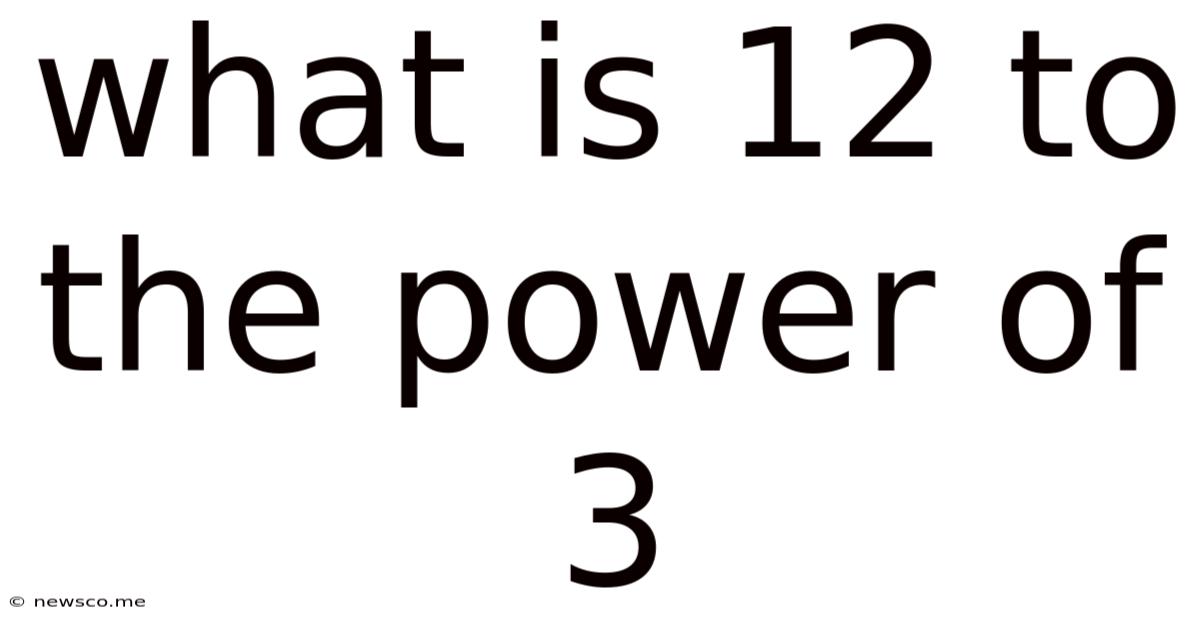
Table of Contents
What is 12 to the Power of 3? A Deep Dive into Exponentiation
Calculating 12 to the power of 3, often written as 12³, might seem like a simple mathematical problem. However, understanding the concept of exponentiation opens doors to a wider world of mathematical concepts and applications, from basic algebra to advanced calculus and even computer science. This article will not only answer the question "What is 12 to the power of 3?" but will also explore the underlying principles of exponents, their practical applications, and related mathematical ideas.
Understanding Exponents: The Basics
Before diving into the specifics of 12³, let's solidify our understanding of exponents. Exponentiation is a mathematical operation that involves raising a number (the base) to a certain power (the exponent). The exponent indicates how many times the base is multiplied by itself. In the general form, a<sup>n</sup>, 'a' is the base and 'n' is the exponent.
For instance:
- 2² (2 to the power of 2 or 2 squared): This means 2 multiplied by itself once: 2 * 2 = 4
- 3³ (3 to the power of 3 or 3 cubed): This means 3 multiplied by itself twice: 3 * 3 * 3 = 27
- 5¹ (5 to the power of 1): Any number raised to the power of 1 is itself: 5
Understanding this fundamental concept is crucial for comprehending more complex mathematical operations.
Calculating 12 Cubed (12³)
Now, let's tackle the question at hand: What is 12 to the power of 3? This means multiplying 12 by itself three times:
12³ = 12 * 12 * 12
Performing the calculation:
12 * 12 = 144 144 * 12 = 1728
Therefore, 12 to the power of 3 is 1728.
Different Methods for Calculation
While simple multiplication works perfectly well for smaller numbers like 12³, other methods exist for calculating exponents, especially when dealing with larger numbers or more complex exponents. These include:
-
Using a Calculator: The most straightforward method, especially for larger numbers or higher exponents. Most calculators have an exponent function (usually denoted as x<sup>y</sup> or ^).
-
Logarithms: Logarithms are the inverse of exponents. They are a powerful tool for solving equations where the unknown is an exponent. However, they are not the most efficient method for simply calculating 12³.
-
Programming Languages: Programming languages like Python, Java, and C++ have built-in functions to calculate exponents efficiently.
Expanding on Exponentiation: Related Concepts and Applications
The concept of exponentiation extends far beyond simple calculations. Let's explore some related mathematical concepts and their real-world applications:
1. Square Roots and Cube Roots
The inverse operation of squaring a number (raising to the power of 2) is finding its square root. Similarly, the inverse operation of cubing a number (raising to the power of 3) is finding its cube root. In our example, the cube root of 1728 is 12.
Finding square roots and cube roots is crucial in various fields, including geometry (calculating areas and volumes), physics (solving equations related to motion and energy), and engineering (designing structures and systems).
2. Scientific Notation
Exponents play a vital role in scientific notation, a way of expressing very large or very small numbers concisely. Scientific notation uses powers of 10 to represent numbers, making them easier to read and manipulate. For instance, the speed of light is approximately 3 x 10⁸ meters per second. This means 3 multiplied by 10 raised to the power of 8 (300,000,000).
3. Compound Interest
In finance, exponentiation is crucial for calculating compound interest. Compound interest is interest earned not only on the principal amount but also on the accumulated interest from previous periods. The formula for compound interest involves exponents, allowing us to calculate the future value of an investment.
4. Exponential Growth and Decay
Many natural phenomena, such as population growth, radioactive decay, and the spread of diseases, can be modeled using exponential functions. These functions use exponents to describe how a quantity changes over time. Understanding exponential growth and decay is essential in various fields, including biology, ecology, and epidemiology.
5. Computer Science
Exponents are fundamental in computer science. They are used in various algorithms, data structures, and computational processes. For instance, binary numbers (the basis of computer systems) use powers of 2. Furthermore, computational complexity, which measures the efficiency of algorithms, often involves exponential functions.
Beyond the Basics: Exploring Higher Powers and Negative Exponents
We've explored 12³, but what about 12 raised to higher powers or even negative powers?
1. Higher Powers
Calculating 12⁴ (12 to the power of 4), 12⁵, and so on, simply involves continuing the multiplication process. For instance:
12⁴ = 12 * 12 * 12 * 12 = 20736
Calculating higher powers quickly becomes more complex, making calculators or programming tools increasingly useful.
2. Negative Exponents
A negative exponent indicates the reciprocal of the base raised to the positive power. For example:
12⁻² = 1 / 12² = 1 / 144
Understanding negative exponents is crucial for simplifying expressions and solving equations in algebra and calculus.
3. Fractional Exponents
Fractional exponents represent roots. For example, 12<sup>1/2</sup> is the square root of 12, and 12<sup>1/3</sup> is the cube root of 12. Fractional exponents are used in various mathematical and scientific applications.
Conclusion: The Significance of 12 Cubed and Exponentiation
While the answer to "What is 12 to the power of 3?" is simply 1728, the journey to reach that answer has unveiled a wealth of mathematical concepts and applications. Exponentiation is a fundamental operation with far-reaching implications in various fields, highlighting its importance in mathematics, science, finance, and computer science. Understanding exponents empowers us to solve complex problems, model real-world phenomena, and appreciate the elegance and power of mathematics. The seemingly simple calculation of 12³ opens a door to a world of mathematical possibilities.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 12 To The Power Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.