What Is .125 In A Fraction
News Co
Mar 26, 2025 · 4 min read
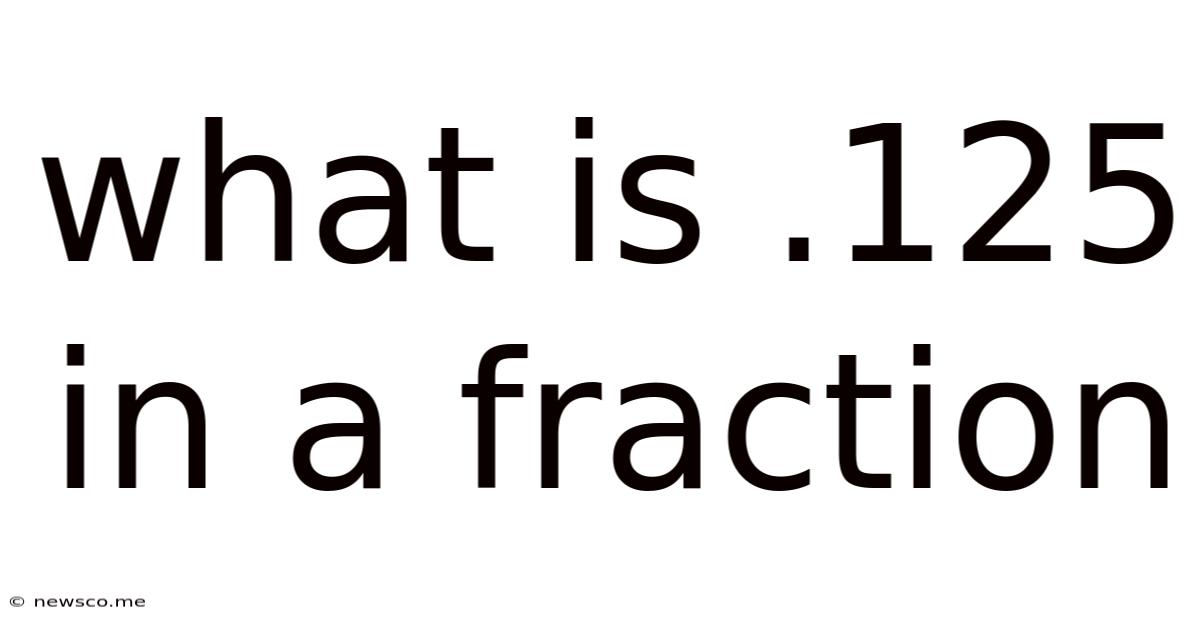
Table of Contents
What is 0.125 as a Fraction? A Comprehensive Guide
Understanding decimal-to-fraction conversions is a fundamental skill in mathematics. This comprehensive guide will delve into the process of converting the decimal 0.125 into a fraction, explaining the steps involved and exploring related concepts. We’ll also examine different approaches and provide practical examples to solidify your understanding.
Understanding Decimal and Fraction Representation
Before we begin the conversion, let's briefly review the meaning of decimals and fractions.
Decimals: Decimals are a way of representing numbers that are not whole numbers. They use a base-ten system, with each digit to the right of the decimal point representing a power of ten. For example, 0.125 represents 1/10 + 2/100 + 5/1000.
Fractions: Fractions represent parts of a whole. They consist of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts, and the denominator indicates the total number of parts the whole is divided into.
Converting 0.125 to a Fraction: The Step-by-Step Process
The conversion of 0.125 to a fraction involves several simple steps:
Step 1: Write the decimal as a fraction with a denominator of 1.
This is the starting point of our conversion. We write 0.125 as:
0.125/1
Step 2: Multiply both the numerator and denominator by a power of 10 to eliminate the decimal point.
To remove the decimal point, we multiply both the numerator and denominator by 1000 (since there are three digits after the decimal point). This is equivalent to multiplying by 10 raised to the power of the number of digits after the decimal point.
(0.125 * 1000) / (1 * 1000) = 125/1000
Step 3: Simplify the fraction.
Now, we simplify the fraction 125/1000 by finding the greatest common divisor (GCD) of the numerator and the denominator. The GCD of 125 and 1000 is 125. We divide both the numerator and the denominator by the GCD:
125 ÷ 125 = 1 1000 ÷ 125 = 8
This gives us the simplified fraction:
1/8
Therefore, 0.125 is equal to 1/8.
Alternative Methods for Conversion
While the above method is straightforward, there are alternative approaches you can use:
Method 1: Recognizing Common Decimal Equivalents
With practice, you'll begin to recognize common decimal-fraction equivalents. Knowing that 0.5 = 1/2, 0.25 = 1/4, and 0.125 = 1/8 can significantly speed up the conversion process.
Method 2: Using a Place Value Chart
A place value chart can be particularly helpful for understanding the relationship between decimal places and fractions. Each place value represents a fraction:
- 0.1 represents 1/10
- 0.01 represents 1/100
- 0.001 represents 1/1000
- and so on.
Using this approach, 0.125 can be expressed as:
(1/10) + (2/100) + (5/1000) = 125/1000, which simplifies to 1/8.
Method 3: Understanding Fractions as Divisions
Every fraction can also be understood as a division problem. The fraction 1/8 is equivalent to 1 divided by 8 (1 ÷ 8 = 0.125). This highlights the inverse relationship between fractions and decimals.
Practical Applications and Real-World Examples
Understanding decimal-to-fraction conversions is crucial in various fields:
-
Cooking and Baking: Many recipes use fractions to indicate amounts of ingredients. Converting decimals to fractions allows for precise measurements. For example, a recipe might call for 1/8 teaspoon of salt instead of 0.125 teaspoon.
-
Engineering and Construction: Precise measurements are essential in engineering and construction. Converting decimals to fractions ensures accuracy in blueprints and designs.
-
Finance: Interest rates, discounts, and stock prices are often expressed as decimals. Converting these decimals to fractions allows for clearer understanding and calculations.
-
Data Analysis: In data analysis, you may encounter data presented in decimal form. Converting to fractions can simplify calculations and interpretations.
-
Everyday Calculations: Many everyday tasks involve fractions and decimals, such as dividing a pizza, sharing items equally, or calculating percentages.
Advanced Concepts and Further Exploration
For a deeper understanding of this topic, consider exploring the following:
-
Recurring Decimals: Decimals that repeat infinitely, such as 0.333..., cannot be expressed as simple fractions. They are known as recurring or repeating decimals and require different conversion methods.
-
Irrational Numbers: Numbers like pi (π) and the square root of 2 (√2) cannot be expressed as fractions. These are known as irrational numbers.
-
Complex Fractions: Complex fractions have fractions in the numerator and/or denominator. Understanding how to simplify complex fractions is important for more advanced mathematical operations.
Conclusion: Mastering Decimal-to-Fraction Conversions
Converting decimals to fractions, as demonstrated with the example of 0.125, is a vital mathematical skill. Understanding the steps involved, along with alternative methods and their applications, empowers you to tackle various mathematical challenges with confidence. Regular practice and exploring related concepts will further enhance your understanding and proficiency in this crucial area of mathematics. By mastering this skill, you’ll not only improve your mathematical abilities but also enhance your problem-solving capabilities across various disciplines. Remember, the key is consistent practice and a solid understanding of the underlying principles. With dedicated effort, you'll find that converting decimals to fractions becomes second nature.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is .125 In A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.