What Is 14 3 As A Mixed Number
News Co
Mar 26, 2025 · 5 min read
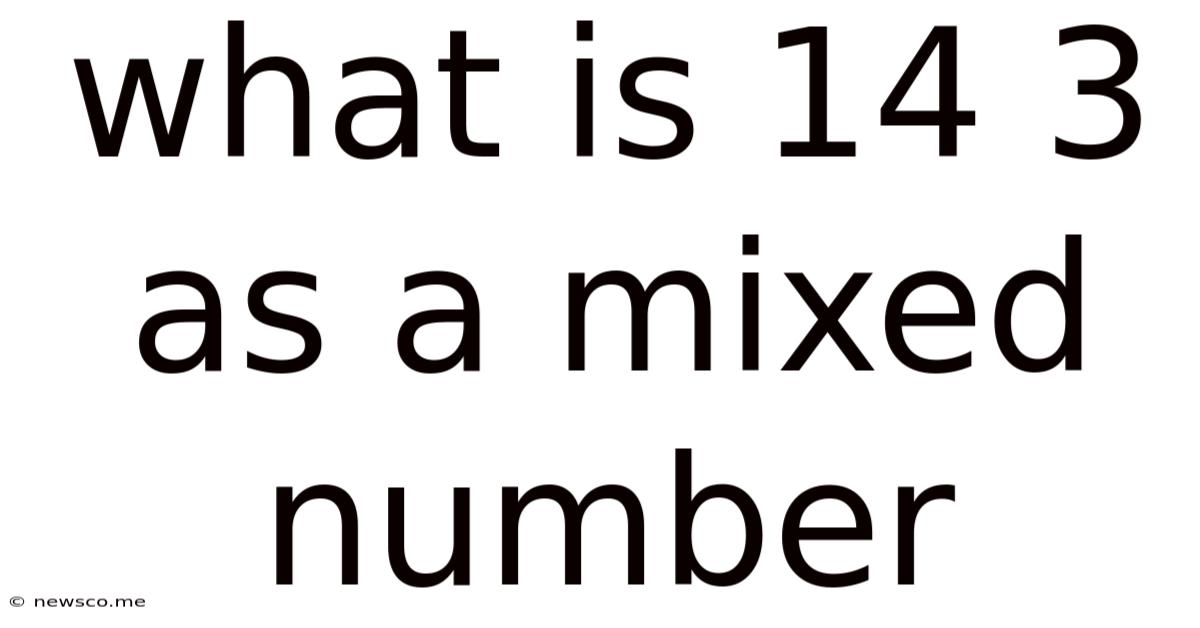
Table of Contents
What is 14/3 as a Mixed Number? A Comprehensive Guide
Understanding fractions and how to convert them into mixed numbers is a fundamental skill in mathematics. This comprehensive guide will not only show you how to convert the improper fraction 14/3 into a mixed number but also delve into the underlying concepts, providing you with a solid understanding of the process and its applications. We'll explore different methods, offer practical examples, and address common questions, ensuring you gain a thorough grasp of this essential mathematical operation.
What are Improper Fractions and Mixed Numbers?
Before we tackle the conversion of 14/3, let's clarify the terminology.
-
Improper Fraction: An improper fraction is a fraction where the numerator (the top number) is greater than or equal to the denominator (the bottom number). Examples include 7/4, 11/5, and, of course, our focus for today, 14/3. The value of an improper fraction is always greater than or equal to 1.
-
Mixed Number: A mixed number combines a whole number and a proper fraction. A proper fraction is one where the numerator is less than the denominator (e.g., 1/2, 3/4, 2/5). Mixed numbers are a convenient way to represent values greater than 1 in a more easily understood format. For example, 2 1/2 is a mixed number representing the sum of the whole number 2 and the fraction 1/2.
Converting 14/3 to a Mixed Number: The Division Method
The most common method for converting an improper fraction to a mixed number involves division. Here's how it works for 14/3:
-
Divide the numerator by the denominator: Divide 14 by 3. This gives you a quotient (the whole number part) and a remainder (the numerator of the fractional part).
14 ÷ 3 = 4 with a remainder of 2
-
Write the mixed number: The quotient becomes the whole number part of the mixed number, and the remainder becomes the numerator of the fractional part. The denominator remains the same as the original denominator.
Therefore, 14/3 as a mixed number is 4 2/3.
Understanding the Process: Why does this work?
This method works because it essentially breaks down the improper fraction into its whole number and fractional components. Think of it visually: you have 14 items, and you want to divide them into groups of 3. You can create 4 complete groups (4 x 3 = 12 items), leaving 2 items leftover (14 - 12 = 2). These 2 leftover items represent the fraction 2/3.
Alternative Method: Repeated Subtraction
While less commonly used, repeated subtraction provides another way to convert an improper fraction to a mixed number. It's a particularly helpful method for visualizing the process.
For 14/3:
-
Subtract the denominator from the numerator repeatedly: Subtract 3 from 14 until the result is less than the denominator (3).
14 - 3 = 11 11 - 3 = 8 8 - 3 = 5 5 - 3 = 2
-
Count the number of subtractions: You performed the subtraction 4 times. This is your whole number.
-
The remaining value is the numerator: The remaining value after the repeated subtraction (2) is your new numerator.
-
Write the mixed number: The whole number (4) and the remaining numerator (2) form the mixed number with the original denominator (3), resulting in 4 2/3.
Practical Applications of Converting Fractions to Mixed Numbers
Converting improper fractions to mixed numbers is crucial in various real-world scenarios:
-
Measurement: When measuring lengths, weights, or volumes, mixed numbers are often more practical and intuitive than improper fractions. For instance, expressing a length as 2 1/2 feet is clearer than 5/2 feet.
-
Cooking and Baking: Recipes frequently use mixed numbers to specify quantities of ingredients. Understanding fraction conversion is essential for accurate measurements.
-
Construction and Engineering: Precision is paramount in construction and engineering, and mixed numbers provide a clear and easily understood way to represent measurements.
-
Everyday Calculations: Many everyday situations involve fractions, and converting them to mixed numbers often simplifies calculations and makes the results more easily interpretable.
Common Mistakes to Avoid
While the conversion process is straightforward, some common errors can occur:
-
Incorrect division: Double-check your division to avoid mistakes in determining the whole number and the remainder.
-
Forgetting the denominator: Ensure the denominator remains consistent throughout the conversion process. It should be the same as the original denominator of the improper fraction.
-
Misinterpreting the remainder: The remainder is crucial; it becomes the numerator of the fractional part of the mixed number.
Further Exploration: Working with Larger Numbers
The same principles apply when dealing with larger numbers. Let's consider an example: Convert 37/5 to a mixed number.
-
Divide: 37 ÷ 5 = 7 with a remainder of 2
-
Write the mixed number: This gives us the mixed number 7 2/5.
You can apply the repeated subtraction method here as well. Subtract 5 from 37 repeatedly until the remainder is less than 5: Seven subtractions will leave a remainder of 2, giving the same result of 7 2/5.
Expanding Your Knowledge: Converting Mixed Numbers to Improper Fractions
The reverse process is equally important. Converting a mixed number back into an improper fraction is often necessary in more advanced mathematical operations. The formula is:
(Whole number * Denominator) + Numerator / Denominator
Let's take our example of 4 2/3:
(4 * 3) + 2 / 3 = 14/3
This shows the equivalence between the mixed number and the improper fraction. This skill is invaluable for performing calculations involving mixed numbers and fractions.
Conclusion
Converting an improper fraction like 14/3 into a mixed number (4 2/3) is a fundamental mathematical skill with far-reaching applications. Understanding the division method and the repeated subtraction approach allows for flexibility and a deeper comprehension of the underlying concepts. By mastering this process and avoiding common mistakes, you build a strong foundation for tackling more complex mathematical problems and effectively apply this knowledge to real-world situations. Remember to practice regularly to solidify your understanding and build confidence in your ability to work comfortably with fractions and mixed numbers.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 14 3 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.