What Is 15 As A Percentage Of 60
News Co
Mar 20, 2025 · 5 min read
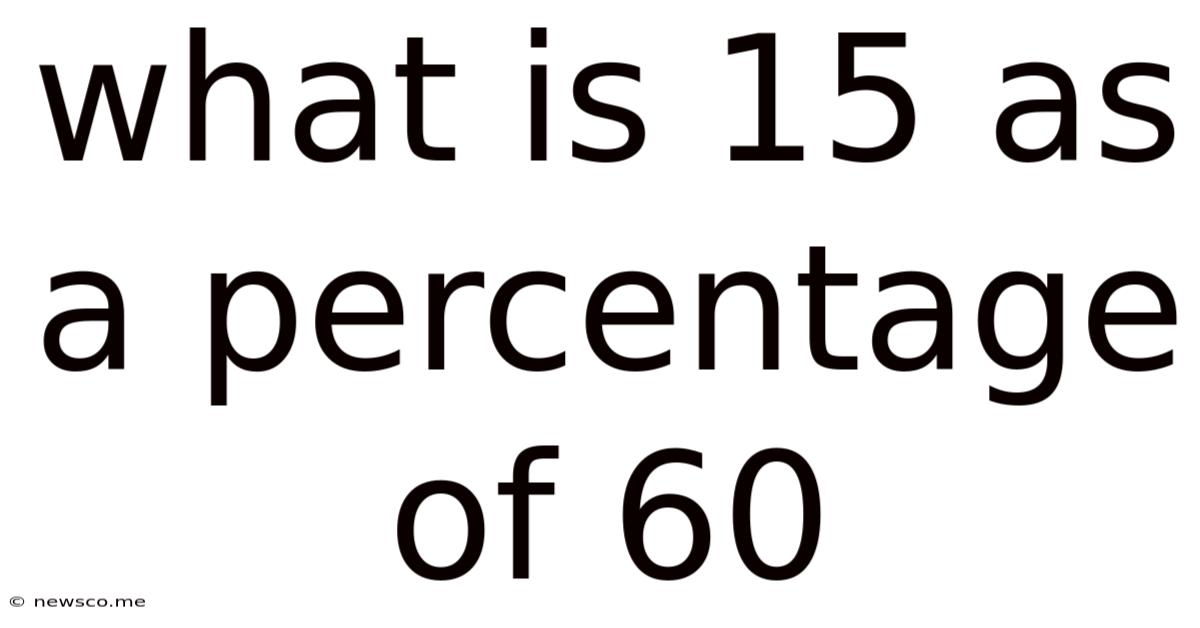
Table of Contents
What is 15 as a Percentage of 60? A Comprehensive Guide
Calculating percentages is a fundamental skill applicable across various fields, from everyday budgeting to complex financial analyses. Understanding how to determine what percentage one number represents of another is crucial for informed decision-making. This comprehensive guide will walk you through calculating "What is 15 as a percentage of 60?" and delve into the broader concept of percentage calculations, providing you with practical applications and helpful tips.
Understanding Percentages
Before we tackle the specific problem, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Calculating 15 as a Percentage of 60: The Step-by-Step Approach
There are several ways to calculate what percentage 15 represents of 60. Here are two common methods:
Method 1: Using the Fraction Method
This method involves expressing the relationship between the two numbers as a fraction and then converting that fraction into a percentage.
-
Form a Fraction: Represent the problem as a fraction: 15/60 (15 is the part, and 60 is the whole).
-
Simplify the Fraction: Simplify the fraction by finding the greatest common divisor (GCD) of 15 and 60. The GCD of 15 and 60 is 15. Divide both the numerator (15) and the denominator (60) by 15: 15/60 simplifies to 1/4.
-
Convert to Decimal: Convert the simplified fraction (1/4) into a decimal by dividing the numerator by the denominator: 1 ÷ 4 = 0.25
-
Convert to Percentage: Multiply the decimal by 100 to express it as a percentage: 0.25 x 100 = 25%
Therefore, 15 is 25% of 60.
Method 2: Using the Formula Method
This method utilizes a direct formula to calculate the percentage. The formula is:
(Part / Whole) x 100% = Percentage
-
Identify the Parts: Identify the "part" (15) and the "whole" (60).
-
Substitute into the Formula: Substitute the values into the formula: (15 / 60) x 100%
-
Calculate: Perform the calculation: (15 / 60) = 0.25; 0.25 x 100% = 25%
Again, the result is 25%.
Practical Applications of Percentage Calculations
Understanding percentage calculations extends beyond simple arithmetic. Here are some practical applications:
- Financial Literacy: Calculating interest rates, discounts, taxes, and profit margins. For example, understanding the percentage increase or decrease in your investments or savings.
- Data Analysis: Interpreting statistical data, such as survey results, market research findings, or scientific experiments. Understanding the percentage of respondents who agree with a particular statement, for instance.
- Business and Sales: Tracking sales performance, calculating commission rates, and analyzing market share. Determining the percentage increase in sales compared to the previous year.
- Everyday Life: Calculating tips in restaurants, understanding discounts on sale items, and determining the percentage of completion on a project. For example, determining what percentage of a project is finished.
- Academic Performance: Calculating grades based on scores obtained in tests and assignments. Calculating the percentage of correct answers in an exam.
Common Percentage Calculation Mistakes to Avoid
While percentage calculations are straightforward, several common mistakes can lead to inaccurate results. These include:
- Incorrect Order of Operations: Remember the order of operations (PEMDAS/BODMAS). Ensure you perform the division before the multiplication when using the formula method.
- Decimal Point Errors: Pay close attention to decimal points when converting between decimals and percentages. An incorrectly placed decimal point can significantly alter the result.
- Confusion with Whole Numbers and Percentages: Avoid confusing the whole number (60 in this case) with the percentage itself.
- Improper Simplification of Fractions: Always simplify fractions to their lowest terms before converting them into decimals and percentages. This simplifies the calculation and reduces the risk of errors.
Expanding Your Understanding: More Complex Percentage Problems
The calculation "What is 15 as a percentage of 60?" serves as a foundation for more complex percentage problems. These problems might involve:
- Finding the Whole: Given a percentage and a part, you can calculate the whole. For example: "25% of what number is 15?"
- Finding the Part: Given a percentage and the whole, you can calculate the part. For example: "What is 25% of 60?"
- Percentage Change: Calculating the percentage increase or decrease between two numbers. For example, "What is the percentage increase from 60 to 75?"
- Compound Percentages: Calculating percentages that build upon each other. For example, calculating the final price after applying successive discounts.
Mastering Percentage Calculations: Tips and Resources
Consistent practice is key to mastering percentage calculations. Here are some tips:
- Start with the Basics: Ensure you have a solid understanding of fractions, decimals, and the concept of percentages before tackling more advanced problems.
- Practice Regularly: Solve a variety of percentage problems to build your confidence and identify areas where you need improvement.
- Use Online Calculators and Tutorials: Online resources can provide additional practice problems and step-by-step explanations.
- Seek Help When Needed: If you're struggling, don't hesitate to seek assistance from a teacher, tutor, or online community.
Conclusion
Calculating "What is 15 as a percentage of 60?" is a simple yet fundamental calculation with broad applications. Mastering this skill enhances your problem-solving abilities and empowers you to approach various situations – from everyday budgeting to complex data analysis – with confidence and accuracy. By understanding the different methods and common pitfalls, you can confidently tackle percentage calculations in any context. Remember, practice makes perfect! Consistent practice will solidify your understanding and make percentage calculations second nature.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 15 As A Percentage Of 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.