What Is 15 Divided By 1 3
News Co
May 02, 2025 · 4 min read
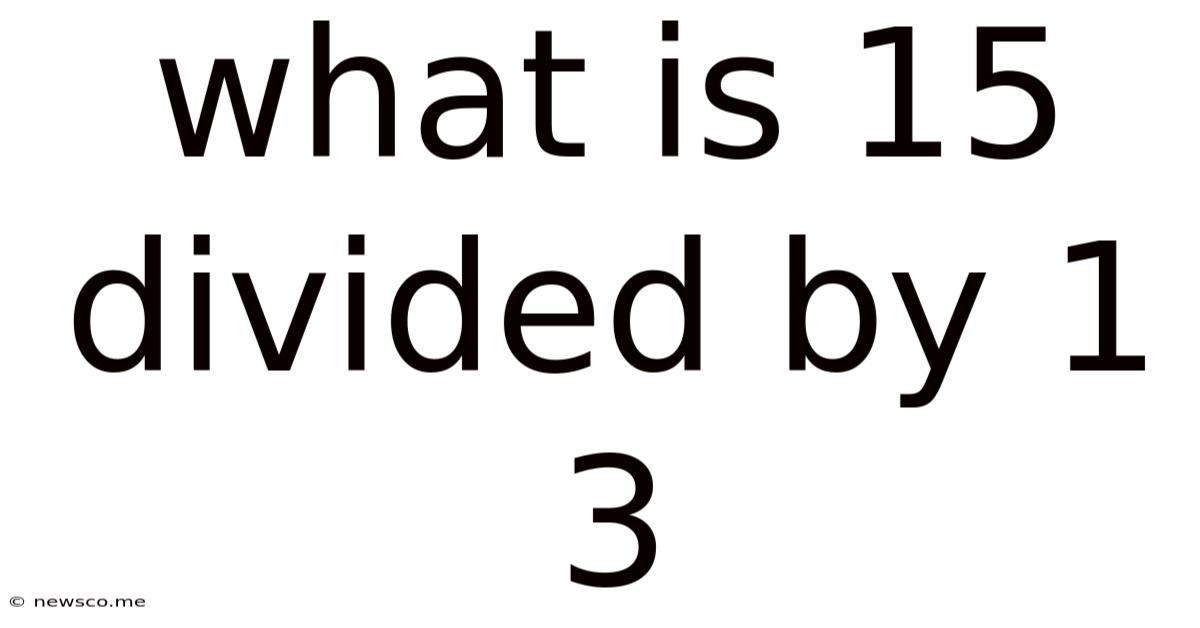
Table of Contents
What is 15 Divided by 1/3? Understanding Fractions and Division
The seemingly simple question, "What is 15 divided by 1/3?" often trips up even those comfortable with basic arithmetic. This article will delve deep into understanding this problem, explaining the concept behind the seemingly counterintuitive answer, and exploring the broader implications of dividing by fractions. We'll cover various methods for solving the problem, addressing common misconceptions, and providing practical applications to solidify your understanding.
Deconstructing the Problem: 15 ÷ (1/3)
At its core, the problem 15 ÷ (1/3) asks: "How many 1/3s are there in 15?" This phrasing helps to visualize the problem and move beyond the abstract nature of dividing by a fraction. Imagine you have 15 pizzas, and you want to divide them into thirds. How many slices (each representing 1/3 of a pizza) will you have?
Misconceptions to Avoid
A common mistake is to incorrectly calculate 15 ÷ (1/3) as 15/3 = 5. This is incorrect because it treats the division as if it were 15 divided by 3, not 15 divided by one-third. Remember, dividing by a fraction is fundamentally different from dividing by a whole number.
Methods for Solving 15 ÷ (1/3)
There are several ways to correctly solve this problem:
Method 1: The "Keep, Change, Flip" Method (Reciprocal Method)
This is arguably the most common and straightforward method. It involves three steps:
- Keep: Keep the first number (the dividend) as it is: 15.
- Change: Change the division sign (÷) to a multiplication sign (×).
- Flip: Flip the second number (the divisor) – find its reciprocal. The reciprocal of 1/3 is 3/1, or simply 3.
Therefore, the problem becomes: 15 × 3 = 45
This method effectively transforms the division problem into a multiplication problem, making it much easier to solve.
Method 2: Visual Representation with a Number Line
Imagine a number line. Each increment represents 1/3. To reach 15, you would need to count how many 1/3 increments are present. Starting at 0, you'd count 1/3, 2/3, 1, 1 1/3, and so on until you reach 15. Counting these increments will reveal there are 45 one-thirds in 15.
This method is particularly helpful for visualizing the concept and solidifying the understanding of what division by a fraction actually represents.
Method 3: Using the Definition of Division
Division can be defined as the inverse operation of multiplication. In other words, a ÷ b = c means that c × b = a. Applying this to our problem:
15 ÷ (1/3) = x
This implies that x × (1/3) = 15. To solve for x, we multiply both sides of the equation by 3:
3 × x × (1/3) = 15 × 3
x = 45
This method demonstrates the underlying mathematical logic behind the "Keep, Change, Flip" method.
Why the Answer is 45: A Deeper Explanation
The answer, 45, makes intuitive sense when you consider that 1/3 is a smaller quantity than 1. Dividing by a number smaller than 1 results in a quotient larger than the dividend. Since we're dividing 15 by a fraction (1/3) that is less than 1, the result (45) will be greater than 15.
Practical Applications of Dividing by Fractions
Understanding division by fractions is crucial in many real-world scenarios:
Cooking and Baking
Recipes often require dividing ingredients into fractions. For example, if a recipe calls for 1/3 cup of sugar and you want to triple the recipe, you need to calculate 3 x (1/3 cup) = 1 cup of sugar.
Construction and Measurement
In construction and carpentry, precise measurements are essential. Dividing lengths of wood or other materials into fractional parts is frequently necessary.
Sewing and Fabric Design
Similar to construction, sewing involves precise measurements. Dividing lengths of fabric into fractions is crucial for creating accurate patterns and garments.
Finance and Budgeting
Dividing budgets into fractional parts to allocate resources effectively is essential for sound financial management.
Data Analysis and Statistics
In data analysis, dividing datasets into fractions for sampling and analysis is common practice. This is vital for drawing accurate conclusions from large datasets.
Expanding the Concept: Dividing by Other Fractions
The principles discussed above apply to dividing by any fraction. For instance, let's consider 15 ÷ (2/5):
- Keep: 15
- Change: ×
- Flip: 5/2
The problem becomes: 15 × (5/2) = 75/2 = 37.5
This highlights the versatility and applicability of the "Keep, Change, Flip" method across various fractional divisions.
Conclusion: Mastering Fraction Division
Understanding how to divide by fractions is a foundational skill in mathematics with widespread applications in various fields. By grasping the underlying concepts and mastering the methods outlined in this article, you'll gain confidence in tackling more complex mathematical problems and solving real-world challenges that involve fractional quantities. Remember to visualize the problem, utilize the "Keep, Change, Flip" method, and always check your work to ensure accuracy. The seemingly simple problem of 15 divided by 1/3 serves as a gateway to a deeper understanding of fractions and their importance in numerical operations. The answer, 45, is not just a numerical result; it's a testament to the power of understanding the intricacies of fractional division.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 15 Divided By 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.