What Is 15 Percent Of 20
News Co
Mar 27, 2025 · 5 min read
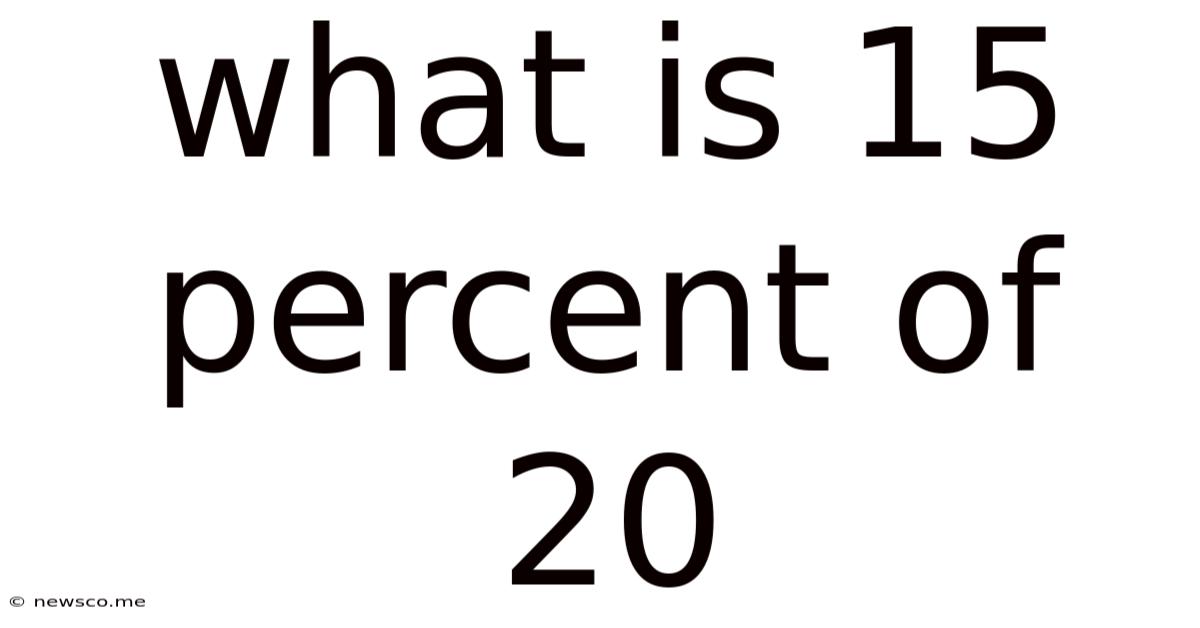
Table of Contents
What is 15 Percent of 20? A Deep Dive into Percentages and Their Applications
The seemingly simple question, "What is 15 percent of 20?" opens a door to a vast world of mathematical concepts and practical applications. While the answer itself is easily calculated (3), understanding the underlying principles and exploring the various ways percentages are used in everyday life offers a richer, more valuable understanding. This article will not only solve this specific problem but will also delve into the mechanics of percentage calculations, explore different methods for solving percentage problems, and demonstrate the wide-ranging uses of percentages across numerous fields.
Understanding Percentages: A Foundation
A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, 15% literally means 15 out of 100, or 15/100. This fractional representation is crucial for understanding how to calculate percentages.
Key Concepts:
- The Whole: This is the total amount or value you're working with. In our example, the whole is 20.
- The Part: This is the portion of the whole that represents the percentage. In this case, we're looking for 15% of 20, so the part is what we need to calculate.
- The Percentage: This is the rate expressed as a number followed by the percent symbol (%). In our example, the percentage is 15%.
Calculating 15% of 20: Three Methods
There are several ways to calculate 15% of 20. Let's explore three common methods:
Method 1: Using the Fractional Representation
As mentioned earlier, 15% can be expressed as the fraction 15/100. To find 15% of 20, we simply multiply the fraction by the whole:
(15/100) * 20 = 3
This method is straightforward and highlights the fundamental concept of percentages as fractions.
Method 2: Converting Percentage to Decimal
Another approach involves converting the percentage to a decimal. To do this, divide the percentage by 100:
15% ÷ 100 = 0.15
Then, multiply the decimal by the whole:
0.15 * 20 = 3
This method is often preferred for its ease of use with calculators.
Method 3: Using Proportions
This method utilizes the concept of proportions. We can set up a proportion where:
x / 20 = 15 / 100
To solve for x (15% of 20), we cross-multiply:
100x = 15 * 20 100x = 300 x = 3
This method is useful for understanding the relationship between the percentage, the part, and the whole.
Beyond the Calculation: Real-World Applications of Percentages
The ability to calculate percentages isn't just an academic exercise; it's a crucial skill applicable in various real-world scenarios. Here are some examples:
1. Financial Calculations:
- Interest Rates: Banks and financial institutions use percentages to calculate interest on loans, savings accounts, and investments. Understanding interest calculations is vital for managing personal finances effectively. For example, calculating the interest earned on a savings account or the total cost of a loan with interest involves percentage calculations.
- Taxes: Sales tax, income tax, and property tax are all expressed as percentages. Accurately calculating taxes requires a firm grasp of percentage calculations.
- Discounts and Sales: Retailers frequently offer discounts expressed as percentages. Knowing how to calculate these discounts is essential for savvy consumers. For instance, a 20% discount on a $100 item means a savings of $20.
- Tips and Gratuities: Calculating tips in restaurants or service charges involves determining a percentage of the total bill.
2. Scientific and Statistical Applications:
- Data Analysis: Percentages are widely used in data analysis to represent proportions, trends, and changes. For example, in surveys and polls, results are often expressed as percentages.
- Probability and Statistics: Probability calculations frequently involve percentages, representing the likelihood of an event occurring.
- Growth Rates: In fields like biology and economics, percentages are used to represent growth rates of populations, economies, or investments over time.
3. Everyday Life:
- Recipe Scaling: Adjusting recipe quantities often involves using percentages. For example, if a recipe calls for 100g of flour and you want to increase it by 15%, you would add 15g of flour (15% of 100g = 15g).
- Grading and Assessment: School grades and test scores are often expressed as percentages. Understanding how percentages are used in grading is important for tracking academic progress.
- Comparisons and Proportions: Percentages allow for easy comparison between different quantities or groups. For instance, comparing the market share of different companies in an industry.
Advanced Percentage Calculations: Beyond the Basics
While calculating 15% of 20 is relatively simple, more complex percentage problems require a deeper understanding. These might involve:
- Finding the Percentage: Determining what percentage one number is of another. For example, what percentage of 20 is 6?
- Finding the Whole: Calculating the original whole given a percentage and the part. For example, if 25% of a number is 10, what is the number?
- Percentage Increase and Decrease: Calculating the percentage change between two numbers. This is crucial for tracking changes over time in various data sets. For instance, calculating the percentage increase in sales from one year to the next.
- Compounding Percentages: Calculating the effect of multiple percentage changes applied sequentially. This is particularly relevant in financial contexts, such as calculating compound interest.
Conclusion: The Power of Percentages
The seemingly simple calculation of "What is 15 percent of 20?" unveils the vast applicability of percentages in our daily lives. From managing finances and interpreting data to scaling recipes and understanding growth rates, the ability to confidently work with percentages is an invaluable skill. Mastering these concepts empowers you to make informed decisions, analyze data effectively, and navigate the quantitative aspects of the world around you. While the answer to the initial question is a straightforward 3, the journey of understanding the underlying principles and applications of percentages is far more enriching and impactful.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Percent Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.