What Is 15 Percent Of 50
News Co
Mar 28, 2025 · 5 min read
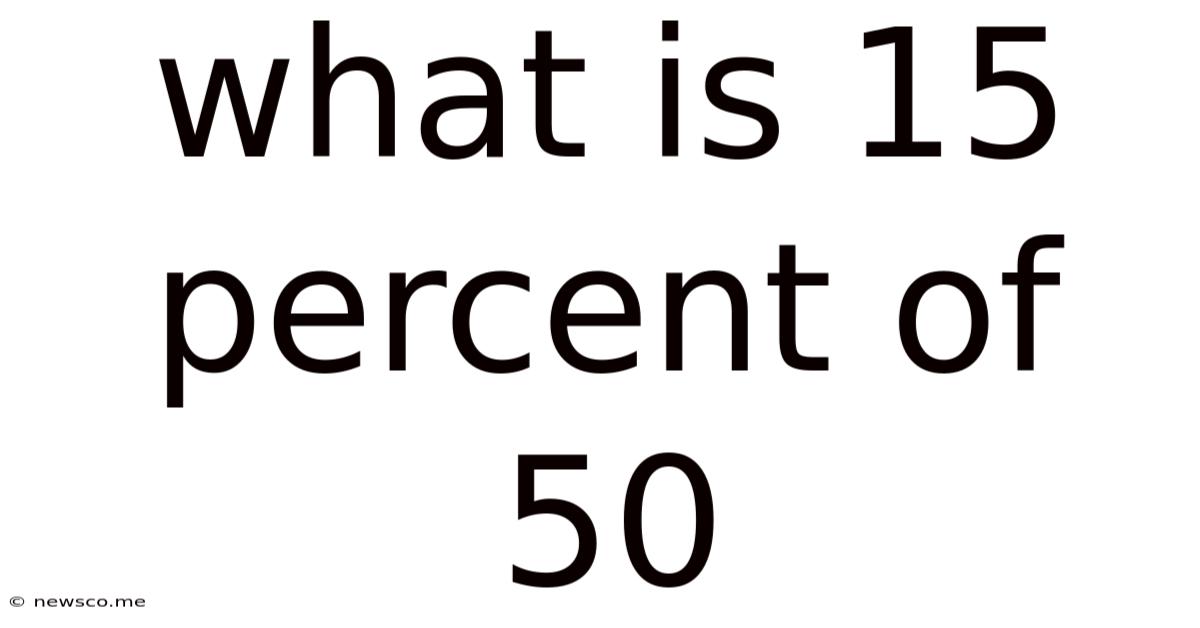
Table of Contents
What is 15 Percent of 50? A Deep Dive into Percentages and Their Applications
Calculating percentages is a fundamental skill with wide-ranging applications in various aspects of life, from everyday finances to complex scientific analyses. Understanding how to determine percentages not only helps us solve specific problems but also enhances our comprehension of proportional relationships and their significance in the world around us. This article delves into the calculation of "What is 15 percent of 50?" and explores the broader implications of percentage calculations.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself is derived from the Latin "per centum," meaning "out of a hundred." Therefore, 15% signifies 15 out of every 100, or 15/100 as a fraction. This fractional representation is key to understanding how percentages work.
Converting Percentages to Decimals and Fractions
To perform calculations involving percentages, it’s often beneficial to convert the percentage to either a decimal or a fraction.
-
Converting to a Decimal: To convert a percentage to a decimal, simply divide the percentage by 100. For example, 15% becomes 15 ÷ 100 = 0.15.
-
Converting to a Fraction: To convert a percentage to a fraction, express the percentage as the numerator and 100 as the denominator. So, 15% becomes 15/100, which can be simplified to 3/20.
Calculating 15% of 50: Three Methods
There are several ways to calculate 15% of 50. Let's explore three common approaches:
Method 1: Using Decimal Conversion
-
Convert the percentage to a decimal: 15% = 0.15
-
Multiply the decimal by the number: 0.15 * 50 = 7.5
Therefore, 15% of 50 is 7.5.
This method is generally the quickest and easiest for most calculations.
Method 2: Using Fraction Conversion
-
Convert the percentage to a fraction: 15% = 15/100 = 3/20
-
Multiply the fraction by the number: (3/20) * 50 = (3 * 50) / 20 = 150/20 = 7.5
Again, we arrive at the answer: 15% of 50 is 7.5. This method is particularly useful when dealing with simpler fractions.
Method 3: Using Proportions
This method is more conceptual and helps visualize the relationship between the percentage, the whole, and the part.
We can set up a proportion:
15/100 = x/50
Where 'x' represents the unknown value (15% of 50).
To solve for x, we cross-multiply:
15 * 50 = 100 * x
750 = 100x
x = 750/100 = 7.5
So, 15% of 50 is 7.5. This approach is valuable for understanding the underlying logic of percentages.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is crucial in many real-life scenarios:
1. Finance and Budgeting:
- Calculating discounts: Determining the actual price of an item after a 15% discount.
- Calculating taxes: Figuring out the amount of sales tax or income tax owed.
- Calculating interest: Determining the interest earned on savings accounts or the interest paid on loans.
- Analyzing investment returns: Understanding the percentage growth or loss of investments.
2. Statistics and Data Analysis:
- Calculating percentages of populations: Determining the percentage of a population with specific characteristics (e.g., percentage of people who prefer a certain product).
- Interpreting survey results: Analyzing survey data to understand the proportions of respondents who hold particular opinions.
- Calculating growth rates: Tracking the percentage increase or decrease in data over time.
3. Science and Engineering:
- Calculating concentrations: Determining the concentration of a substance in a solution (e.g., 15% saline solution).
- Analyzing experimental data: Expressing experimental results as percentages to facilitate comparison.
4. Everyday Life:
- Calculating tips: Determining the appropriate tip amount in a restaurant.
- Understanding sales: Evaluating the savings offered during sales promotions.
- Managing household budgets: Tracking spending and allocating resources based on percentages.
Beyond the Basics: More Complex Percentage Calculations
While calculating 15% of 50 is a straightforward example, more complex percentage problems frequently arise. These often involve finding the percentage, the whole, or a part when only some of these values are known.
Finding the Percentage:
If you know the part and the whole, you can calculate the percentage using the formula:
Percentage = (Part / Whole) * 100
For example, if 12 is a part of 60, the percentage is (12/60) * 100 = 20%.
Finding the Whole:
If you know the part and the percentage, you can find the whole using the formula:
Whole = (Part / Percentage) * 100
For example, if 15 is 25% of a whole number, then the whole is (15/25) * 100 = 60.
Percentage Increase and Decrease:
Calculating percentage increases or decreases involves finding the difference between two numbers and expressing it as a percentage of the original number.
- Percentage Increase: [(New Value - Original Value) / Original Value] * 100
- Percentage Decrease: [(Original Value - New Value) / Original Value] * 100
Mastering Percentages: Practice and Resources
The best way to master percentage calculations is through consistent practice. Start with simple problems, gradually increasing the complexity. Many online resources, including educational websites and practice apps, offer interactive exercises and quizzes to help you hone your skills.
Conclusion
Understanding how to calculate percentages is a valuable skill with far-reaching implications. From managing personal finances to interpreting scientific data, the ability to accurately and efficiently calculate percentages is essential in various aspects of daily life. By mastering the fundamentals and exploring the different methods of calculation, you can confidently tackle a wide range of percentage problems and use this knowledge to make informed decisions. The simple calculation of “What is 15 percent of 50?” serves as a foundational stepping stone to understanding a much broader and more significant mathematical concept.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 15 Percent Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.