What Is 15 Percent Of 60
News Co
Mar 20, 2025 · 5 min read
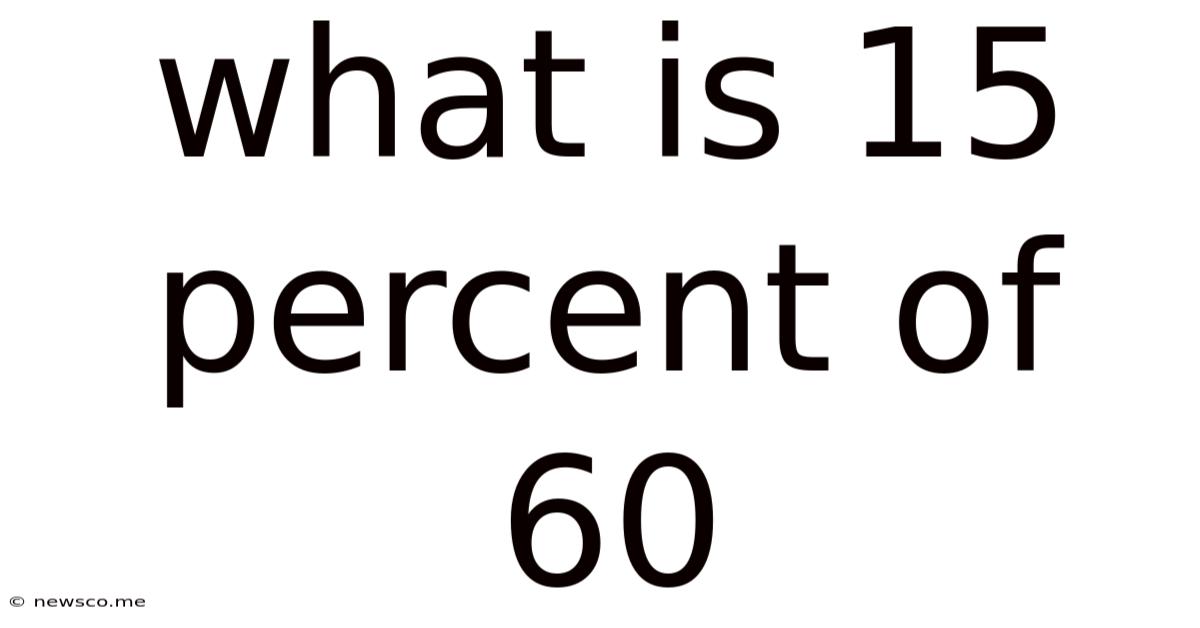
Table of Contents
What is 15 Percent of 60? A Deep Dive into Percentage Calculations
Calculating percentages is a fundamental skill applicable across various aspects of life, from budgeting and shopping to understanding financial reports and academic assessments. This seemingly simple question – "What is 15 percent of 60?" – opens the door to exploring different calculation methods, their applications, and the broader concept of percentages themselves.
Understanding Percentages
Before delving into the calculation, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100." Therefore, 15% means 15 out of 100, or 15/100.
This fundamental understanding is crucial because it allows us to translate percentages into decimals and fractions, making calculations easier and more intuitive.
Method 1: Converting Percentage to Decimal
This is arguably the most straightforward method. We convert the percentage to its decimal equivalent and then multiply it by the number.
Step 1: Convert the Percentage to a Decimal
To convert 15% to a decimal, we divide it by 100:
15% ÷ 100 = 0.15
Step 2: Multiply the Decimal by the Number
Now, we multiply the decimal by 60:
0.15 * 60 = 9
Therefore, 15% of 60 is 9.
This method is efficient and easily adaptable to various percentage calculations. It's particularly useful when using calculators or spreadsheets.
Method 2: Using Fractions
This method leverages the fractional representation of percentages. We convert the percentage to a fraction and then multiply it by the number.
Step 1: Convert Percentage to a Fraction
15% can be expressed as the fraction 15/100.
Step 2: Simplify the Fraction (Optional)
We can simplify the fraction by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 5:
15/100 = 3/20
Step 3: Multiply the Fraction by the Number
Now, we multiply the simplified fraction by 60:
(3/20) * 60 = 180/20 = 9
Therefore, 15% of 60 is 9.
This method offers a deeper understanding of the underlying mathematical principles. It's especially helpful in situations where mental calculation is preferred or when dealing with fractions in other contexts.
Method 3: Using the Proportion Method
This method uses proportions to solve for the unknown value. We set up a proportion where one ratio represents the percentage and the other represents the part to the whole.
Step 1: Set up the Proportion
We can set up the proportion as follows:
15/100 = x/60
Where 'x' represents the unknown value (15% of 60).
Step 2: Cross-Multiply and Solve
Cross-multiplying gives us:
100x = 15 * 60
100x = 900
x = 900/100
x = 9
Therefore, 15% of 60 is 9.
This method is particularly useful in more complex percentage problems where multiple variables are involved. It provides a structured approach to solving for the unknown.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is vital in numerous real-world scenarios:
-
Retail Sales: Calculating discounts, sales tax, and final prices. For example, a 15% discount on a $60 item would result in a $9 discount, making the final price $51.
-
Finance: Determining interest earned or paid, calculating loan repayments, and understanding financial statements. For instance, earning 15% interest on a $60 investment would yield $9 in interest.
-
Academic Assessments: Calculating grades based on weighted averages, understanding test scores, and evaluating performance metrics. A score of 15 out of 60 would represent a 25% grade (15/60 = 0.25 or 25%).
-
Data Analysis: Interpreting data sets, calculating percentages of various attributes, and representing data graphically. For example, if 15 out of 60 respondents chose a particular option, it represents 25% of the total respondents.
-
Everyday Budgeting: Allocating funds for different expenses, tracking savings progress, and managing personal finances. For example, allocating 15% of a $60 budget for groceries would result in $9 dedicated to groceries.
Advanced Percentage Calculations and Concepts
While this article focuses on a simple percentage calculation, understanding the underlying principles allows you to tackle more complex scenarios:
-
Calculating Percentage Increase/Decrease: This involves determining the percentage change between two values. For instance, if a value increases from 60 to 69, the percentage increase is calculated as [(69-60)/60] * 100 = 15%.
-
Calculating Percentage Points: This is distinct from percentage change. It refers to the absolute difference between two percentages. For example, if interest rates rise from 5% to 20%, the increase is 15 percentage points.
-
Working Backwards from a Percentage: Determining the original value when only the percentage and resulting value are known. For example, if 15% of a number is 9, then the original number is calculated as 9 / (15/100) = 60.
-
Compound Interest: Calculating interest that accrues not only on the principal but also on accumulated interest. This is a more advanced concept used extensively in finance.
-
Percentage Points vs. Percentage Change: A common point of confusion is the difference between a percentage change and percentage points. A percentage change is a relative comparison, while percentage points are an absolute difference.
Conclusion
Calculating 15% of 60, seemingly straightforward, serves as a springboard to understanding the broader world of percentage calculations. Mastering these calculations empowers you to confidently navigate various aspects of daily life, from personal finance to professional endeavors. By understanding the different methods and their real-world applications, you gain a valuable skill applicable in countless situations. Remember to practice regularly and explore more advanced concepts to hone your proficiency and expand your mathematical understanding. The ability to work confidently with percentages is a skill that offers substantial benefits in various spheres of life.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 15 Percent Of 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.