What Is 2 3 Of 24
News Co
Apr 03, 2025 · 5 min read
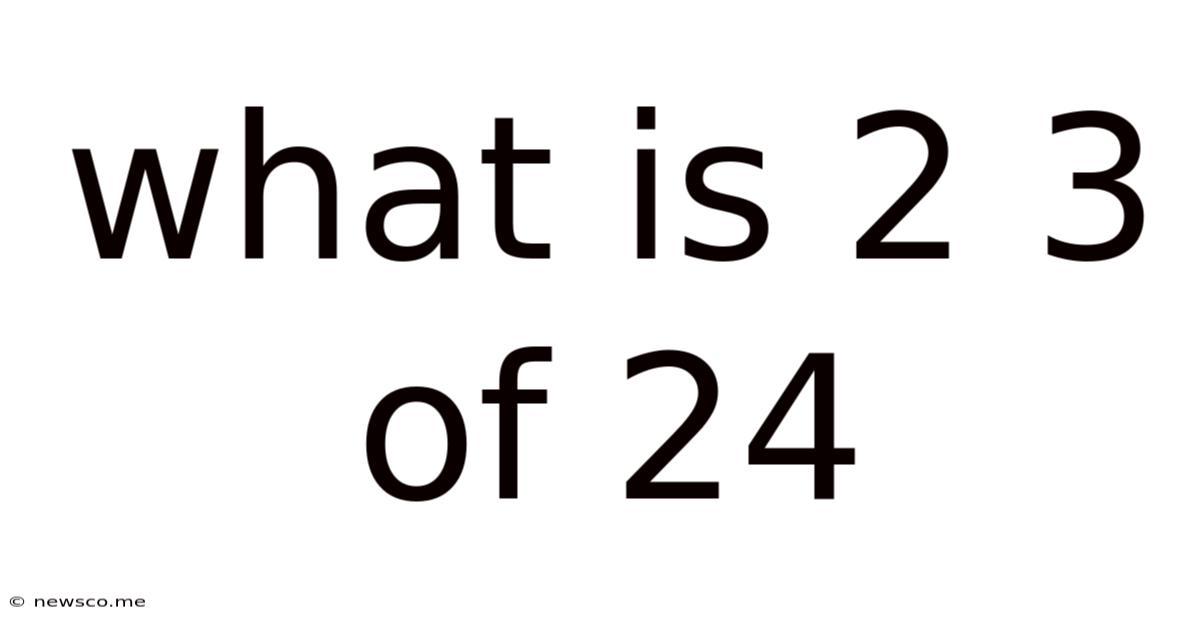
Table of Contents
What is 2/3 of 24? A Comprehensive Guide to Fractions and Their Applications
This seemingly simple question, "What is 2/3 of 24?", opens the door to a fascinating exploration of fractions, their practical applications, and the underlying mathematical concepts. While the answer itself is straightforward, understanding the why behind the calculation is crucial for mastering more complex fractional problems. This guide will not only answer the question but delve deep into the methodology, providing you with a solid foundation in fractional arithmetic.
Understanding Fractions: The Building Blocks
Before we tackle the problem, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts you have, and the denominator indicates how many equal parts the whole is divided into.
For instance, in the fraction 2/3, 2 is the numerator and 3 is the denominator. This means we have 2 parts out of a total of 3 equal parts.
Calculating 2/3 of 24: The Step-by-Step Approach
There are several ways to calculate 2/3 of 24. Let's explore the most common methods:
Method 1: Multiplication
This is the most straightforward method. To find a fraction of a number, we multiply the fraction by the number. In this case:
(2/3) * 24
To perform this multiplication, we can:
- Multiply the numerator by the whole number: 2 * 24 = 48
- Divide the result by the denominator: 48 / 3 = 16
Therefore, 2/3 of 24 is 16.
Method 2: Division and Multiplication (Simplified)
We can simplify the process by dividing the whole number by the denominator first, and then multiplying by the numerator.
- Divide the whole number by the denominator: 24 / 3 = 8
- Multiply the result by the numerator: 8 * 2 = 16
This method often leads to smaller numbers, making the calculation easier, especially with larger numbers. Again, we arrive at the answer: 16.
Method 3: Visual Representation
Imagine you have 24 items, and you want to find 2/3 of them.
- Divide the whole into equal parts: Divide 24 items into 3 equal groups. Each group will contain 24 / 3 = 8 items.
- Take the required number of parts: You need 2 out of the 3 parts, so take 2 groups of 8 items. 2 * 8 = 16 items.
This visual approach helps solidify the concept of fractions and makes the calculation more intuitive.
Beyond the Basics: Expanding Our Understanding
Now that we've found the answer, let's delve deeper into related concepts and applications to further enhance our understanding of fractions.
1. Equivalent Fractions:
The fraction 2/3 is equivalent to many other fractions, such as 4/6, 6/9, 8/12, and so on. These fractions represent the same proportion, although they use different numerators and denominators. Understanding equivalent fractions is crucial for simplifying fractions and performing operations with them.
2. Improper Fractions and Mixed Numbers:
An improper fraction is one where the numerator is greater than or equal to the denominator (e.g., 5/3). A mixed number combines a whole number and a proper fraction (e.g., 1 2/3). It's important to know how to convert between these forms, as this is often necessary in solving complex fraction problems.
3. Fraction Operations:
Understanding how to add, subtract, multiply, and divide fractions is essential for advanced applications. These operations involve finding common denominators, simplifying fractions, and applying the appropriate rules of arithmetic.
4. Real-World Applications:
Fractions are ubiquitous in everyday life. They are used in:
- Cooking and Baking: Following recipes often involves working with fractions of ingredients.
- Measurement: Measuring lengths, weights, and volumes often requires dealing with fractions.
- Finance: Calculating percentages, interest rates, and discounts involves fractional arithmetic.
- Construction: Many construction projects rely on precise measurements, which often involve fractions.
- Data Analysis: Fractions are used extensively in representing proportions and ratios in data sets.
5. Percentage Equivalents:
Fractions can easily be converted into percentages. To convert 2/3 into a percentage, we divide the numerator by the denominator and multiply by 100:
(2/3) * 100 ≈ 66.67%
This highlights the interrelationship between fractions, decimals, and percentages, showing how they are different representations of the same proportional concept.
Advanced Applications: Taking it Further
Let's explore some more advanced scenarios that build upon the fundamental understanding of fractions:
1. Solving Word Problems:
Many real-world problems involve fractions. Consider this example: "A farmer harvests 24 bushels of apples. He sells 2/3 of his harvest. How many bushels did he sell?" This is essentially the same problem we started with, but in a contextualized form.
2. Working with Multiple Fractions:
Problems might involve multiple fractions. For example, "A baker uses 1/4 cup of sugar for one recipe and 2/3 cup of sugar for another. How much sugar did he use in total?" Solving these problems requires a solid understanding of fraction addition.
3. Applications in Geometry and Algebra:
Fractions play a significant role in geometry (calculating areas and volumes) and algebra (solving equations and inequalities). Understanding fractional concepts is crucial for mastering these subjects.
Conclusion: Mastering Fractions for a Brighter Future
The seemingly simple question, "What is 2/3 of 24?", serves as a springboard to a much broader understanding of fractions and their wide-ranging applications. By mastering the basic concepts and extending your knowledge to more complex scenarios, you'll equip yourself with a powerful tool for navigating the numerical world. From everyday tasks to advanced mathematical concepts, a firm grasp of fractions is essential for academic success and practical problem-solving in numerous fields. Remember to practice regularly, explore different methods of calculation, and apply your knowledge to real-world situations to solidify your understanding and build confidence in your mathematical abilities. The journey to mastering fractions is a rewarding one, and the skills you acquire will serve you well throughout your life.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 2 3 Of 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.