What Is 2 3 Of 9
News Co
Mar 26, 2025 · 5 min read
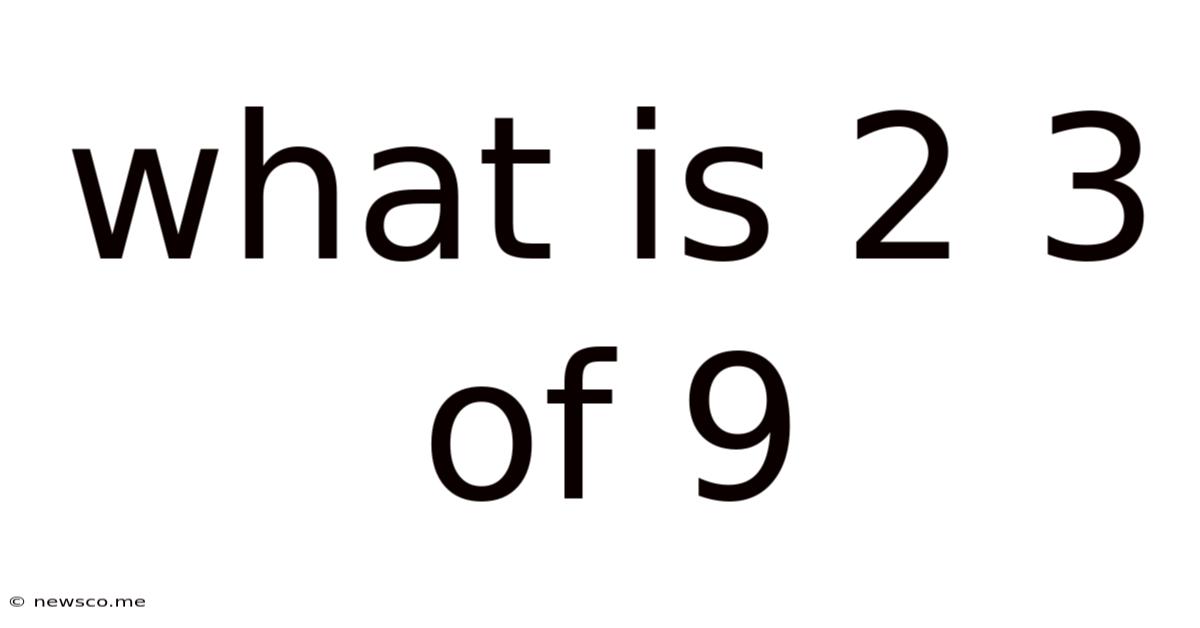
Table of Contents
What is 2/3 of 9? A Comprehensive Guide to Fractions and Their Applications
The question, "What is 2/3 of 9?" might seem simple at first glance, but it opens the door to a deeper understanding of fractions, their manipulation, and their practical applications in various fields. This article will not only answer this specific question but also explore the broader concepts of fractions, providing a comprehensive guide suitable for students, educators, and anyone seeking to strengthen their mathematical foundation.
Understanding Fractions: A Building Block of Mathematics
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 2/3, 2 is the numerator and 3 is the denominator. This means we have 2 parts out of a total of 3 equal parts.
Key Concepts Related to Fractions
- Proper Fraction: A fraction where the numerator is smaller than the denominator (e.g., 2/3, 1/4).
- Improper Fraction: A fraction where the numerator is greater than or equal to the denominator (e.g., 5/3, 4/4).
- Mixed Number: A combination of a whole number and a proper fraction (e.g., 1 2/3). This represents a whole plus a fractional part.
- Equivalent Fractions: Fractions that represent the same value, even though they have different numerators and denominators (e.g., 1/2 = 2/4 = 3/6). These are created by multiplying or dividing both the numerator and denominator by the same number (excluding zero).
- Simplifying Fractions: Reducing a fraction to its lowest terms by dividing both the numerator and denominator by their greatest common divisor (GCD). For example, 6/9 simplifies to 2/3 because the GCD of 6 and 9 is 3.
Calculating 2/3 of 9: A Step-by-Step Approach
Now, let's tackle the original question: What is 2/3 of 9? This can be interpreted as finding 2/3 multiplied by 9. There are several ways to solve this:
Method 1: Multiplication
The most straightforward method is to multiply the fraction by the whole number:
(2/3) * 9 = (2 * 9) / 3 = 18 / 3 = 6
Therefore, 2/3 of 9 is 6.
Method 2: Dividing then Multiplying
We can also break down the problem into two steps:
- Divide: Divide the whole number (9) by the denominator (3): 9 / 3 = 3. This tells us that one-third of 9 is 3.
- Multiply: Multiply the result (3) by the numerator (2): 3 * 2 = 6. This gives us two-thirds of 9.
This method is particularly helpful when dealing with larger numbers or more complex fractions.
Method 3: Visual Representation
Imagine a circle divided into three equal parts. Each part represents 1/3 of the whole. To find 2/3, we simply shade two of these parts. Since each part represents 9/3 = 3, two parts represent 3 * 2 = 6.
This visual approach is excellent for building intuitive understanding, especially for beginners.
Practical Applications of Fractions: Beyond the Classroom
Fractions are not confined to textbooks; they are fundamental to various real-world scenarios. Understanding how to work with fractions is crucial in:
1. Cooking and Baking:
Recipes often require fractional measurements of ingredients. For instance, a recipe might call for 2/3 cup of sugar or 1/4 teaspoon of salt. Accurate fraction calculations ensure the recipe turns out as intended.
2. Construction and Engineering:
Precise measurements are essential in construction and engineering. Fractions are used extensively in blueprints, calculations for material quantities, and ensuring accurate dimensions.
3. Finance and Budgeting:
Understanding fractions is critical for managing personal finances. Calculating discounts, interest rates, and proportions of income allocated to different expenses all involve working with fractions. For example, figuring out how much you save when an item is marked down by 1/3 of its original price.
4. Data Analysis and Statistics:
Fractions are used to represent proportions and percentages in data analysis and statistics. This is crucial for interpreting survey results, understanding probability, and making informed decisions based on data. For example, representing the proportion of respondents who favored a particular option in a poll.
5. Science and Measurement:
In science, precise measurements often involve fractions. Scientists use fractions to represent quantities, ratios, and concentrations of substances in experiments and data analysis.
Advanced Fraction Concepts and Operations
Beyond the basic calculations, several other concepts involving fractions are crucial for a complete understanding:
1. Adding and Subtracting Fractions:
To add or subtract fractions, they must have a common denominator. If they don't, find the least common multiple (LCM) of the denominators and convert the fractions to equivalent fractions with the LCM as the new denominator. Then, add or subtract the numerators while keeping the denominator the same.
2. Multiplying Fractions:
Multiplying fractions is relatively straightforward. Multiply the numerators together and then multiply the denominators together. Simplify the resulting fraction if necessary.
3. Dividing Fractions:
To divide fractions, invert (reciprocate) the second fraction (the divisor) and then multiply the two fractions.
4. Converting Between Fractions, Decimals, and Percentages:
Fractions can be easily converted to decimals by dividing the numerator by the denominator. To convert a decimal to a percentage, multiply by 100 and add the % symbol. Conversely, percentages can be converted to fractions by dividing by 100 and simplifying. These conversions are vital for flexibility in problem-solving.
5. Solving Equations Involving Fractions:
Many mathematical problems involve solving equations containing fractions. Techniques for solving such equations typically involve clearing fractions by multiplying both sides of the equation by the least common denominator.
Conclusion: Mastering Fractions for a Brighter Future
The seemingly simple question, "What is 2/3 of 9?", serves as a gateway to a wide world of mathematical concepts and their practical applications. A solid grasp of fractions is not merely a requirement for academic success but a valuable skill that empowers individuals to navigate various aspects of life, from everyday tasks to complex professional endeavors. By understanding the fundamental principles, mastering the operations, and appreciating the diverse applications of fractions, we unlock a greater ability to analyze, solve problems, and make informed decisions in a world increasingly reliant on numerical reasoning. Therefore, continue practicing, exploring, and applying your knowledge of fractions—the rewards are limitless.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 2 3 Of 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.