What Is 2.5 Percent As A Decimal
News Co
Apr 24, 2025 · 4 min read
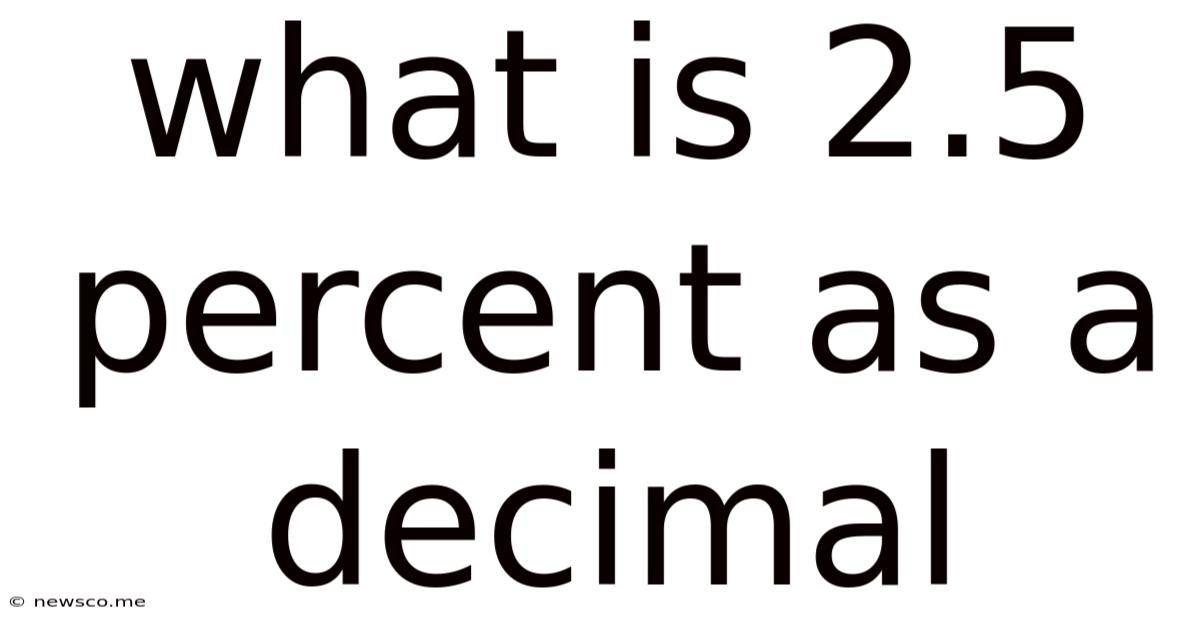
Table of Contents
What is 2.5 Percent as a Decimal? A Comprehensive Guide
Understanding percentage conversions is fundamental in various fields, from finance and mathematics to everyday life. This article will delve deep into the conversion of 2.5 percent to its decimal equivalent, explaining the process step-by-step and providing further insights into percentage-to-decimal conversions in general. We'll explore practical applications and answer common questions surrounding this conversion. This comprehensive guide aims to solidify your understanding of percentages and decimals, equipping you with the knowledge to tackle similar conversions confidently.
Understanding Percentages and Decimals
Before we jump into the conversion of 2.5 percent to a decimal, let's establish a clear understanding of what percentages and decimals represent.
Percentages: A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Decimals: A decimal is a way of expressing a number as a fraction where the denominator is a power of 10 (10, 100, 1000, and so on). The decimal point separates the whole number part from the fractional part. For example, 0.5 represents 5/10, and 0.75 represents 75/100.
The core relationship between percentages and decimals lies in their representation of parts of a whole. Both express fractions but in different forms. Converting between them is a crucial skill in numerical analysis.
Converting 2.5 Percent to a Decimal: The Step-by-Step Process
The conversion of 2.5% to a decimal involves a straightforward two-step process:
Step 1: Convert the Percentage to a Fraction
To start, remember that a percentage is a fraction with a denominator of 100. So, 2.5% can be written as:
2.5/100
Step 2: Convert the Fraction to a Decimal
To convert a fraction to a decimal, we simply divide the numerator (the top number) by the denominator (the bottom number):
2.5 ÷ 100 = 0.025
Therefore, 2.5% as a decimal is 0.025.
Practical Applications of Percentage-to-Decimal Conversion
The ability to convert percentages to decimals is essential in numerous real-world applications:
-
Finance: Calculating interest rates, discounts, taxes, and profit margins frequently requires converting percentages to decimals. For example, calculating simple interest on a loan requires the interest rate (expressed as a percentage) to be converted to a decimal.
-
Statistics: Percentages are often used to represent data in statistical analysis. Converting them to decimals is necessary for various statistical calculations, such as calculating means, standard deviations, and probabilities.
-
Science: In scientific fields, percentages are used to express concentrations, errors, and changes. Converting to decimals is crucial for precise calculations and data representation.
-
Everyday Life: Understanding percentage-to-decimal conversions helps in everyday tasks such as calculating tips, understanding sale discounts, and comparing prices.
Beyond 2.5%: A General Approach to Percentage-to-Decimal Conversion
The method used to convert 2.5% to a decimal applies universally to any percentage. The key is to understand the underlying principle: divide the percentage by 100.
Here's a generalized approach:
-
Write the percentage as a fraction with a denominator of 100. For example, X% becomes X/100.
-
Divide the numerator by the denominator. This will give you the decimal equivalent.
Examples:
- 15%: 15/100 = 0.15
- 7.2%: 7.2/100 = 0.072
- 125%: 125/100 = 1.25
- 0.5%: 0.5/100 = 0.005
Common Mistakes to Avoid
While the conversion process is straightforward, some common mistakes can occur:
-
Incorrect placement of the decimal point: When dividing by 100, remember that this moves the decimal point two places to the left. Failing to do this correctly is a frequent error.
-
Forgetting to divide by 100: Some may mistakenly treat the percentage as the decimal equivalent. Remember, the crucial step is always to divide by 100.
-
Misinterpreting percentages greater than 100%: Percentages above 100% result in decimals greater than 1. Understanding this is essential for accurate calculations.
Advanced Applications and Further Exploration
The conversion of percentages to decimals extends beyond basic calculations. It forms the foundation for more complex mathematical operations and concepts such as:
-
Compound interest: Calculating compound interest involves repeated percentage calculations, which necessitate converting percentages to decimals.
-
Exponential growth and decay: These concepts often utilize percentages to represent growth or decay rates, requiring decimal conversions for accurate modeling.
-
Statistical inference: Many statistical methods require decimal representations of percentages for precise analysis and interpretation of data.
Conclusion: Mastering Percentage-to-Decimal Conversions
This comprehensive guide has provided a thorough explanation of converting 2.5 percent to its decimal equivalent (0.025), along with a detailed understanding of the general process for any percentage. Mastering this fundamental conversion is crucial for success in various fields and everyday life. By understanding the underlying principles and avoiding common pitfalls, you can confidently handle percentage-to-decimal conversions and apply this knowledge to a wide range of applications, from simple calculations to complex mathematical modeling. Remember the core principle: divide the percentage by 100 to obtain the decimal equivalent. This simple yet powerful tool empowers you to navigate numerical tasks efficiently and accurately.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 2.5 Percent As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.