What Is 2.875 As A Fraction
News Co
Apr 19, 2025 · 4 min read
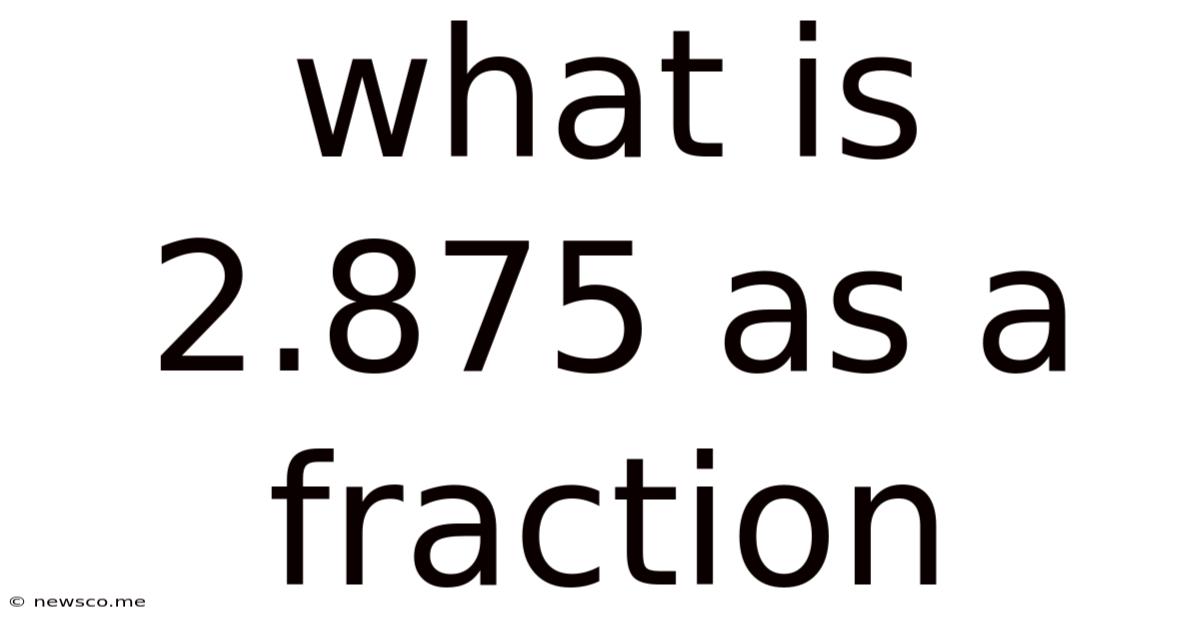
Table of Contents
What is 2.875 as a Fraction? A Comprehensive Guide
Converting decimals to fractions might seem daunting at first, but with a systematic approach, it becomes straightforward. This comprehensive guide will walk you through the process of converting the decimal 2.875 into a fraction, explaining the underlying principles and offering valuable insights into decimal-to-fraction conversions in general. We'll cover multiple methods, ensuring you understand the "why" behind the calculations, not just the "how."
Understanding Decimal Places and Fraction Equivalents
Before diving into the conversion, let's refresh our understanding of decimal places. The decimal point separates the whole number part from the fractional part. In 2.875, the '2' represents the whole number, while '.875' represents the fractional part. Each digit after the decimal point represents a power of ten:
- .8 represents 8 tenths (8/10)
- .07 represents 7 hundredths (7/100)
- .005 represents 5 thousandths (5/1000)
Therefore, 2.875 can be thought of as 2 + 8/10 + 7/100 + 5/1000. Our goal is to combine these fractional parts into a single fraction.
Method 1: Using the Place Value Method
This is a direct and intuitive method. We observe that the decimal 0.875 extends to the thousandths place. This implies that the denominator of our fraction will be 1000. The numerator is simply the decimal part without the decimal point, which is 875.
Therefore, 0.875 = 875/1000.
Since we have the whole number 2, we add it to our fraction: 2 + 875/1000. To express this as a single improper fraction, we convert the whole number to an equivalent fraction with a denominator of 1000: (2 * 1000)/1000 = 2000/1000.
Adding the fractions: 2000/1000 + 875/1000 = 2875/1000
This improper fraction represents 2.875. However, it's generally preferred to simplify fractions to their lowest terms.
Method 2: Simplifying the Fraction
To simplify 2875/1000, we need to find the greatest common divisor (GCD) of the numerator and the denominator. The GCD is the largest number that divides both 2875 and 1000 without leaving a remainder. One way to find the GCD is through prime factorization.
Prime factorization of 2875: 5³ x 23 Prime factorization of 1000: 2³ x 5³
The common factors are 5³. Therefore, the GCD is 5³ = 125.
Now, we divide both the numerator and the denominator by the GCD:
2875 ÷ 125 = 23 1000 ÷ 125 = 8
Therefore, the simplified fraction is 23/8. This is the most concise and commonly accepted representation of 2.875 as a fraction.
Method 3: Converting to a Mixed Number
While 23/8 is an improper fraction (numerator is larger than the denominator), it's also common to express it as a mixed number. This involves dividing the numerator by the denominator:
23 ÷ 8 = 2 with a remainder of 7
This means 23/8 can be written as 2 and 7/8, or 2 7/8. This clearly shows the whole number part (2) and the fractional part (7/8).
Choosing the Best Representation
The best representation of 2.875 as a fraction depends on the context. For mathematical calculations, the improper fraction 23/8 might be more convenient. For everyday understanding and communication, the mixed number 2 7/8 might be more intuitive.
Practical Applications and Real-World Examples
Understanding decimal-to-fraction conversions is essential in various fields:
- Cooking and Baking: Recipes often require precise measurements, and converting decimal measurements into fractional ones is crucial for accuracy.
- Engineering and Construction: Precise calculations are paramount in these fields, and fractions are often used in blueprint readings and calculations.
- Finance: Calculations involving interest rates, shares, and currency exchange often require fraction conversions.
- Science: Many scientific measurements and calculations utilize fractions, particularly when dealing with small quantities.
Advanced Decimal-to-Fraction Conversions
The methods discussed above primarily focus on terminating decimals (decimals with a finite number of digits). Converting recurring decimals (decimals with repeating digits) to fractions requires a slightly different approach, involving algebraic manipulation. For example, converting 0.333... (recurring 3) to a fraction involves setting up an equation and solving for the unknown.
Let x = 0.333... 10x = 3.333... Subtracting the first equation from the second: 9x = 3, therefore x = 1/3.
Conclusion: Mastering Decimal to Fraction Conversions
Converting decimals like 2.875 to fractions is a fundamental skill with broad applications. By understanding the underlying principles of place value, prime factorization, and the different methods for simplification, you can confidently tackle such conversions. Remember to choose the most appropriate representation – improper fraction or mixed number – depending on the context and the specific needs of your calculation or problem. Mastering this skill will significantly enhance your mathematical abilities and improve your understanding of numerical relationships. The ability to seamlessly switch between decimal and fractional forms allows for greater flexibility and accuracy in diverse fields and applications. This skill is not just about solving problems; it's about building a deeper understanding of numbers and their representations.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 2.875 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.