What Is 2 Times 3 4
News Co
Apr 10, 2025 · 6 min read
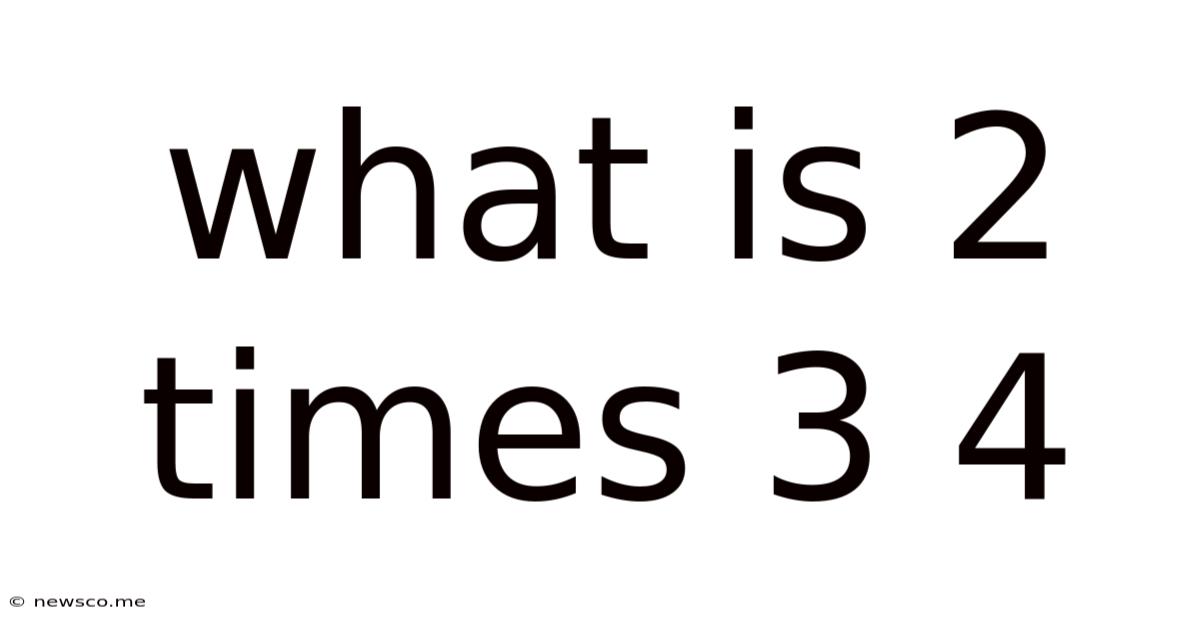
Table of Contents
What is 2 Times 34? Exploring Multiplication and its Applications
The seemingly simple question, "What is 2 times 34?", opens a door to a vast world of mathematical concepts and practical applications. While the answer itself is straightforward – 68 – the journey to understanding how we arrive at that answer reveals fundamental principles of multiplication and its widespread use in various fields. This article will delve deep into this seemingly basic calculation, exploring the underlying mathematical principles, different methods of solving it, and the diverse ways multiplication impacts our daily lives.
Understanding Multiplication: The Foundation
At its core, multiplication is a shorthand way of performing repeated addition. When we say "2 times 34," we're essentially asking: what is the sum of 34 added to itself twice? This can be expressed as 34 + 34 = 68. This basic understanding forms the bedrock of more complex multiplication problems.
The Commutative Property: Order Doesn't Matter
One crucial aspect of multiplication is the commutative property. This property states that the order of the numbers being multiplied does not affect the result. Therefore, 2 times 34 is the same as 34 times 2. Both operations yield the same answer: 68. This seemingly simple property is fundamental to simplifying calculations and understanding algebraic manipulations.
The Associative Property: Grouping Numbers
The associative property allows us to group numbers in multiplication without changing the outcome. This is particularly useful when dealing with more than two numbers. For instance, if we want to calculate (2 x 3) x 4, we can either multiply 2 and 3 first (resulting in 6) and then multiply by 4 (resulting in 24), or we can multiply 3 and 4 first (resulting in 12) and then multiply by 2 (again resulting in 24). The grouping doesn't change the final product.
Different Methods for Calculating 2 Times 34
While the addition method (34 + 34) is perfectly valid for this specific problem, several other methods offer efficiency, especially when dealing with larger numbers.
The Standard Algorithm: A Step-by-Step Approach
The standard algorithm, taught in most schools, involves multiplying each digit of the second number (34) by the first number (2) and then adding the results.
- Step 1: Multiply 2 by the units digit of 34 (4): 2 x 4 = 8
- Step 2: Multiply 2 by the tens digit of 34 (3): 2 x 3 = 6
- Step 3: Combine the results: 68
Mental Math Techniques: Quick Calculations
With practice, mental math techniques can significantly speed up calculations. For 2 times 34, one could double each digit separately: double 30 is 60, and double 4 is 8. Adding these together (60 + 8) gives 68.
Using Distributive Property: Breaking Down the Problem
The distributive property allows us to break down complex multiplications into simpler ones. We can rewrite 34 as (30 + 4). Then, we apply the distributive property:
2 x (30 + 4) = (2 x 30) + (2 x 4) = 60 + 8 = 68
This method is particularly useful when dealing with larger numbers or those that are easily divisible.
The Significance of Multiplication: Real-World Applications
The seemingly simple calculation of 2 times 34 extends far beyond the classroom. Multiplication is fundamental to countless real-world scenarios, impacting our daily lives in profound ways.
Everyday Finances: Budgeting and Shopping
From calculating the total cost of groceries to determining the monthly payment on a loan, multiplication is essential for managing personal finances. If you buy two items costing $34 each, you instantly use multiplication to find the total cost.
Measurement and Conversions: Units of Measurement
Converting units of measurement frequently involves multiplication. For example, if a recipe calls for 34 grams of flour and you need to double the recipe, you would use multiplication to determine the total amount of flour needed (2 x 34 = 68 grams). Similar conversions are used across various units, like length, volume, and weight.
Engineering and Construction: Precise Calculations
In engineering and construction, precise calculations are vital for safety and efficiency. Whether calculating the amount of materials needed for a building project or determining the load-bearing capacity of a structure, multiplication is indispensable.
Science and Data Analysis: Statistical Calculations
Scientific research and data analysis heavily rely on multiplication. Calculating averages, determining probabilities, and performing statistical analyses all involve multiple multiplications.
Computer Science and Programming: Algorithms and Data Structures
Multiplication forms the basis of many algorithms and data structures in computer science. From image processing to encryption, these underlying mathematical principles are crucial for the functionality of software and hardware.
Business and Economics: Profit, Loss, and Growth
Business and economic calculations extensively utilize multiplication. Determining profit margins, calculating sales tax, or forecasting growth rates all rely on this fundamental operation. For instance, if a business sells 34 units of a product at $2 each, the total revenue is calculated through multiplication (34 x $2 = $68).
Expanding the Understanding: Beyond 2 Times 34
While this article focuses on the specific calculation of "2 times 34," the principles discussed are transferable to more complex mathematical problems. Understanding the underlying concepts of multiplication, such as the commutative and associative properties, as well as the different calculation methods, builds a solid foundation for more advanced mathematical concepts.
Exploring Larger Numbers: Multiplication with Multi-Digit Numbers
The techniques discussed earlier – the standard algorithm, mental math, and the distributive property – can be extended to handle multiplications involving larger numbers. This involves a deeper understanding of place value and the systematic application of multiplication rules.
Introduction to Algebra: Variables and Equations
Multiplication is a key component of algebra. Instead of using specific numbers, algebraic equations use variables to represent unknown quantities. Understanding multiplication helps solve equations and manipulate algebraic expressions.
Geometry and its Applications: Area, Volume, and more
Multiplication is central to many geometric calculations. Finding the area of a rectangle (length x width), the volume of a cube (side x side x side), or calculating the circumference of a circle all rely heavily on multiplication.
Conclusion: The Pervasiveness of Multiplication
The seemingly simple question, "What is 2 times 34?", unveils a rich tapestry of mathematical concepts and their widespread applications. From everyday calculations to complex scientific models, multiplication is a cornerstone of mathematics and a fundamental tool for navigating the world around us. Mastering this basic operation and understanding its underlying principles opens doors to a broader understanding of mathematics and its significant role in numerous fields. By understanding the methods and applications discussed in this article, you’ll be well-equipped to tackle more complex calculations and appreciate the power of this fundamental mathematical operation. It's not just about getting the answer (68); it's about understanding why the answer is 68 and how that understanding unlocks a world of possibilities.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 2 Times 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.