What Is 2 To The Negative 3rd Power
News Co
Apr 26, 2025 · 4 min read
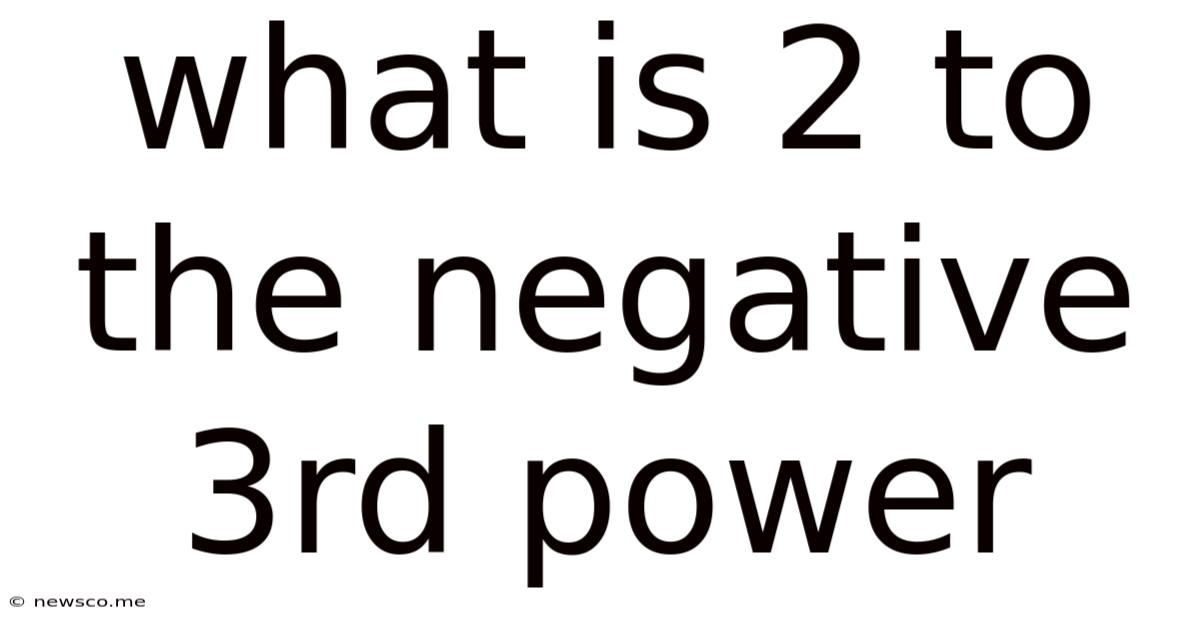
Table of Contents
What is 2 to the Negative 3rd Power? A Comprehensive Guide
Understanding exponents, particularly negative exponents, is crucial for anyone delving into mathematics, science, or even computer programming. This comprehensive guide will thoroughly explore the meaning of 2 to the negative 3rd power (2⁻³), explaining the concept, providing step-by-step calculations, and showcasing its practical applications. We'll also delve into the broader context of negative exponents and their relationship to positive exponents, fractions, and reciprocals.
Understanding Exponents
Before tackling negative exponents, let's solidify our understanding of positive exponents. An exponent, also known as a power or index, indicates how many times a base number is multiplied by itself. For example:
- 2³ (2 to the power of 3 or 2 cubed) means 2 × 2 × 2 = 8.
- 5² (5 to the power of 2 or 5 squared) means 5 × 5 = 25.
- 10⁴ (10 to the power of 4) means 10 × 10 × 10 × 10 = 10,000.
The base number is the number being multiplied, and the exponent tells us how many times to multiply it.
Deciphering Negative Exponents
Now, let's introduce the concept of negative exponents. A negative exponent signifies the reciprocal of the base raised to the positive power. In simpler terms, it means "one over" the base raised to the positive exponent. Therefore:
a⁻ⁿ = 1/aⁿ
This rule applies to any base 'a' (except 0, as division by zero is undefined) and any exponent 'n'.
Calculating 2 to the Negative 3rd Power (2⁻³)
Applying the rule above to our problem, 2⁻³, we get:
2⁻³ = 1/2³
Now, we calculate 2³:
2³ = 2 × 2 × 2 = 8
Therefore:
2⁻³ = 1/8
This is the final answer. 2 to the negative 3rd power is equal to one-eighth (0.125 in decimal form).
Visualizing Negative Exponents
It can be helpful to visualize negative exponents in the context of a pattern. Let's observe the powers of 2:
- 2⁴ = 16
- 2³ = 8
- 2² = 4
- 2¹ = 2
- 2⁰ = 1 (Any number raised to the power of 0 is 1)
- 2⁻¹ = 1/2 = 0.5
- 2⁻² = 1/2² = 1/4 = 0.25
- 2⁻³ = 1/2³ = 1/8 = 0.125
- 2⁻⁴ = 1/2⁴ = 1/16 = 0.0625
Notice the pattern: as the exponent decreases by 1, the value is halved. This pattern continues for both positive and negative exponents.
Practical Applications of Negative Exponents
Negative exponents aren't just abstract mathematical concepts; they appear frequently in various fields:
Science and Engineering:
- Scientific Notation: Negative exponents are essential for representing very small numbers in scientific notation. For example, the size of an atom might be expressed as 10⁻¹⁰ meters.
- Physics: Many physics equations involve negative exponents, especially those dealing with inverse relationships (like inverse square laws in gravity and electromagnetism).
- Chemistry: Concentrations of substances in solutions are often expressed using negative exponents in molarity calculations.
Computer Science:
- Data Storage: Data sizes are often expressed using powers of 2 (kilobytes, megabytes, gigabytes, etc.). Negative exponents can be used to represent very small data sizes.
- Algorithms: Some algorithms and data structures utilize negative exponents in their computational processes.
Finance:
- Compound Interest: While usually expressed positively, the concept of compounding interest over time can be explained and calculated more accurately utilizing exponents, both positive and negative to reflect growth or decay of an investment.
Further Exploration of Exponent Rules
Understanding negative exponents is part of a larger picture involving various exponent rules. These rules help simplify calculations involving exponents:
- Product of Powers: aᵐ × aⁿ = aᵐ⁺ⁿ (add the exponents when multiplying powers with the same base)
- Quotient of Powers: aᵐ / aⁿ = aᵐ⁻ⁿ (subtract the exponents when dividing powers with the same base)
- Power of a Power: (aᵐ)ⁿ = aᵐⁿ (multiply the exponents when raising a power to another power)
- Power of a Product: (ab)ᵐ = aᵐbᵐ (distribute the exponent to each factor within the parenthesis)
- Power of a Quotient: (a/b)ᵐ = aᵐ/bᵐ (distribute the exponent to both the numerator and denominator)
These rules, when used in conjunction with the understanding of negative exponents, significantly enhance your ability to solve complex mathematical problems.
Common Mistakes to Avoid
When working with negative exponents, some common errors can occur:
- Misinterpreting the Reciprocal: Remember that a negative exponent doesn't make the entire expression negative. It makes the expression the reciprocal of the base raised to the positive exponent.
- Incorrect Application of Exponent Rules: Carefully follow the exponent rules mentioned above to avoid errors in calculations. Double-check your steps.
- Confusing Negative Exponents with Negative Bases: The negative sign in the exponent has a different meaning than a negative sign within the base. For example, (-2)³ is -8, while 2⁻³ is 1/8.
Conclusion
Mastering the concept of negative exponents, like 2⁻³, is a significant step towards fluency in mathematics. It opens doors to more advanced mathematical concepts and their applications in various scientific and technological fields. By understanding its meaning, applying the relevant rules, and avoiding common mistakes, you can confidently tackle problems involving negative exponents and contribute to a more robust understanding of exponential expressions. Remember to practice regularly and build upon this foundation to further develop your mathematical proficiency. This will not only improve your mathematical skills but also enhance your problem-solving capabilities across various disciplines.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 2 To The Negative 3rd Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.