What Is 2 To The Power Of 4
News Co
Mar 15, 2025 · 6 min read
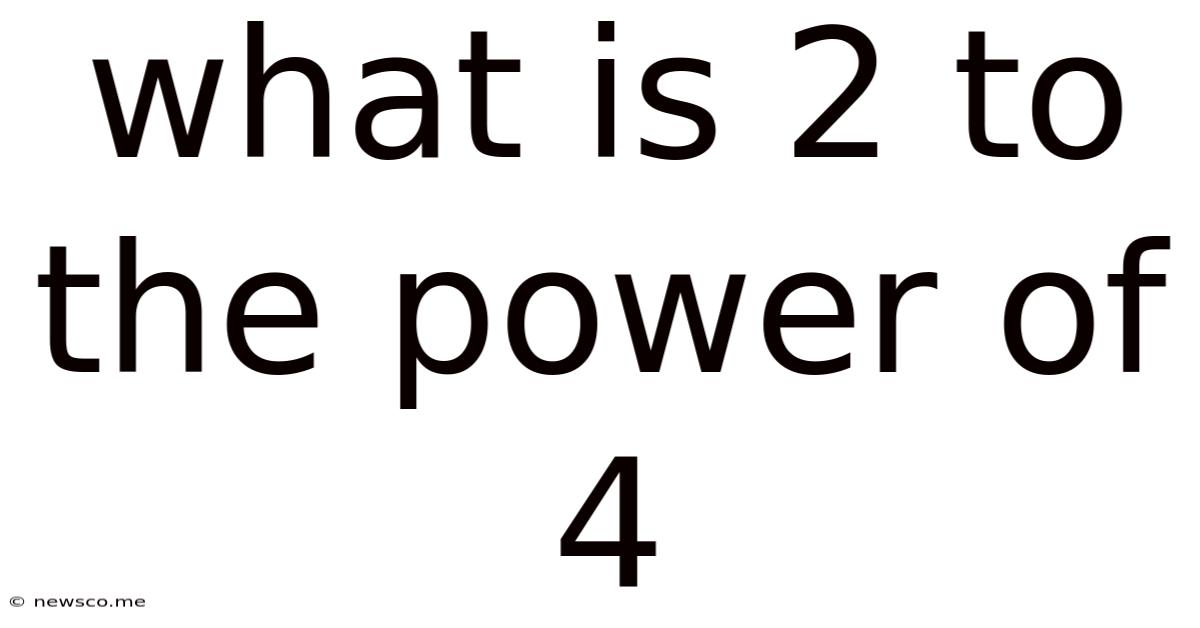
Table of Contents
What is 2 to the Power of 4? A Deep Dive into Exponents and Their Applications
The seemingly simple question, "What is 2 to the power of 4?", opens a door to a vast world of mathematical concepts, practical applications, and fascinating historical context. While the answer itself is straightforward (16), understanding the underlying principles and exploring the broader implications of exponents offers significant value for anyone interested in mathematics, computer science, finance, or indeed, any field that deals with growth and scaling.
Understanding Exponents: The Fundamentals
Before diving into the specifics of 2<sup>4</sup>, let's solidify our understanding of exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. In the expression b<sup>n</sup>, 'b' is the base and 'n' is the exponent. This means b<sup>n</sup> represents b multiplied by itself 'n' times.
For example:
- 2<sup>3</sup> = 2 × 2 × 2 = 8 (2 multiplied by itself three times)
- 5<sup>2</sup> = 5 × 5 = 25 (5 multiplied by itself two times)
- 10<sup>1</sup> = 10 (10 multiplied by itself one time – just 10)
- 10<sup>0</sup> = 1 (Any non-zero number raised to the power of 0 is 1. This is a crucial rule in exponent mathematics.)
Therefore, 2<sup>4</sup> = 2 × 2 × 2 × 2 = 16. The answer to our initial question is simply 16.
Beyond the Simple Calculation: Exploring the Significance of 2<sup>4</sup>
While the numerical answer is easily obtained, the significance of 2<sup>4</sup> extends far beyond this basic calculation. Let's examine some of its implications:
1. Binary Numbers and Computer Science
The number 16 holds significant weight in computer science due to its relationship with the binary number system. The binary system is a base-2 system, using only two digits (0 and 1) to represent all numbers. Understanding powers of 2 is crucial for working with binary, as each bit (binary digit) represents a power of 2.
- 16 in binary is 10000. This is because 16 = 2<sup>4</sup>. The leftmost digit represents 2<sup>4</sup> (16), the next 2<sup>3</sup> (8), then 2<sup>2</sup> (4), 2<sup>1</sup> (2), and 2<sup>0</sup> (1). In this case, only the leftmost digit is '1', representing 2<sup>4</sup>, while all other digits are '0', indicating the absence of those powers of 2.
This foundational understanding of powers of 2 is essential for programmers, computer engineers, and anyone working with digital data.
2. Exponential Growth and Decay
The concept of 2<sup>4</sup> exemplifies exponential growth. Exponential growth is a pattern where a quantity increases at a rate proportional to its current value. This type of growth is common in various scenarios, including:
- Population Growth: In a simplified model, if a population doubles every year, the size after four years would be calculated using 2<sup>4</sup>.
- Compound Interest: The growth of an investment earning compound interest follows an exponential pattern. Understanding exponents allows for the calculation of future investment values.
- Viral Spread: The spread of information or disease can often be modeled using exponential growth functions.
Conversely, the inverse of exponential growth is exponential decay, where a quantity decreases at a rate proportional to its current value. This can model phenomena like radioactive decay or the depreciation of assets.
3. Combinatorics and Probability
Powers of 2 frequently appear in combinatorics, the branch of mathematics dealing with combinations and permutations. Consider a scenario with four binary choices (yes/no, on/off, true/false). The total number of possible combinations is 2<sup>4</sup> = 16. This type of combinatorial analysis is vital in various fields, including:
- Genetics: Determining the number of possible genetic combinations.
- Cryptography: Analyzing the security of encryption algorithms.
- Network Design: Evaluating the number of possible network configurations.
4. Geometric Progressions
The calculation 2<sup>4</sup> is also deeply connected to geometric progressions. A geometric progression is a sequence where each term is the product of the previous term and a constant value (the common ratio). In the case of 2<sup>4</sup>, the geometric progression is: 2, 4, 8, 16, where the common ratio is 2. Geometric progressions have numerous applications in finance, physics, and engineering.
Expanding the Scope: Powers of 2 and Their Importance
The simple calculation of 2<sup>4</sup> serves as a stepping stone to understanding the broader implications of powers of 2. These powers play a crucial role in numerous fields:
- Data Storage: Hard drive capacities are often expressed in powers of 2 (kilobytes, megabytes, gigabytes, etc.).
- Memory Management: Computer memory is organized and addressed using powers of 2.
- Music Theory: The octave in music involves a doubling of frequency, directly relating to powers of 2.
- Game Development: Game mechanics and level design often incorporate powers of 2 for efficient data representation and processing.
Understanding powers of 2 is not merely an academic exercise; it's a fundamental concept with far-reaching practical applications in a wide array of fields.
Further Exploration: Beyond 2<sup>4</sup>
The exploration of exponents doesn't end with 2<sup>4</sup>. Understanding the properties of exponents allows us to tackle more complex calculations and solve more intricate problems. Here are some key concepts to further enhance your understanding:
- Negative Exponents: A negative exponent means reciprocal. For instance, 2<sup>-4</sup> = 1/2<sup>4</sup> = 1/16.
- Fractional Exponents: Fractional exponents represent roots. For example, 2<sup>1/2</sup> is the square root of 2, and 2<sup>1/3</sup> is the cube root of 2.
- Exponential Functions: These functions involve variables as exponents, like y = 2<sup>x</sup>. Their graphs show the characteristic exponential growth or decay curves.
- Logarithms: Logarithms are the inverse of exponential functions. They provide a way to solve for exponents in equations.
Conclusion: The Power of Understanding 2<sup>4</sup>
While the immediate answer to "What is 2 to the power of 4?" is simply 16, the true significance of this question lies in the underlying concepts of exponents and their vast applications. From binary arithmetic in computer science to exponential growth models in finance and the world of combinatorics, understanding exponents provides a powerful tool for solving problems and gaining insights across numerous disciplines. The seemingly straightforward calculation of 2<sup>4</sup> opens the door to a wealth of mathematical knowledge and its significant impact on our understanding of the world around us. Continuing to explore exponents and their related concepts is an investment in enhancing your mathematical literacy and problem-solving skills, paving the way for success in various fields.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 2 To The Power Of 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.