What Is 20 Of 10 Dollars
News Co
Apr 15, 2025 · 5 min read
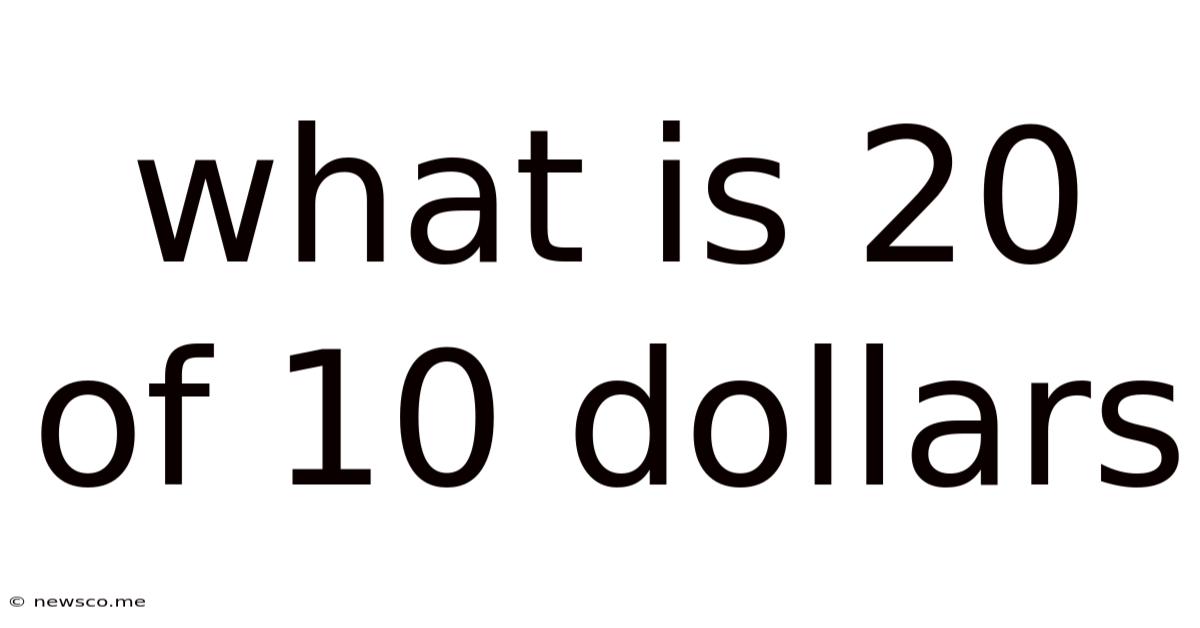
Table of Contents
What is 20% of 10 Dollars? A Deep Dive into Percentages and Their Real-World Applications
Calculating percentages might seem like a simple arithmetic task, but understanding its applications extends far beyond the classroom. From calculating sales tax and discounts to understanding financial reports and even baking, percentages are an integral part of our daily lives. This article delves into the seemingly straightforward question: "What is 20% of 10 dollars?" and then explores the broader context of percentage calculations, their practical uses, and how to master them.
Understanding Percentages: A Foundation
Before tackling the specific problem, let's solidify our understanding of percentages. A percentage is a fraction or a ratio expressed as a number out of 100. The symbol "%" represents "per cent," which literally means "out of one hundred." So, 20% means 20 out of 100, or 20/100, which simplifies to 1/5.
This foundational understanding is crucial because it allows us to convert percentages into decimals and fractions, making calculations much easier. To convert a percentage to a decimal, simply divide the percentage by 100. For example, 20% becomes 0.20 (or 0.2). To convert a decimal to a percentage, multiply by 100 and add the "%" symbol.
Calculating 20% of 10 Dollars: The Solution
Now, let's address the question at hand: What is 20% of 10 dollars? We can solve this problem using several methods:
Method 1: Decimal Conversion
- Convert the percentage to a decimal: 20% = 0.20
- Multiply the decimal by the total amount: 0.20 x $10 = $2
Therefore, 20% of 10 dollars is $2.
Method 2: Fraction Conversion
- Convert the percentage to a fraction: 20% = 20/100 = 1/5
- Multiply the fraction by the total amount: (1/5) x $10 = $2
Again, we arrive at the answer: $2.
Method 3: Using Proportion
This method is particularly useful for more complex percentage problems. We can set up a proportion:
20/100 = x/$10
Solving for x (the unknown amount):
100x = 200 x = $2
The answer remains consistent: $2.
Real-World Applications of Percentage Calculations
The ability to calculate percentages efficiently has numerous practical applications across various aspects of life:
1. Finance and Budgeting:
- Calculating interest: Understanding interest rates on loans, savings accounts, and investments requires proficiency in percentage calculations.
- Determining discounts: Sales, coupons, and promotional offers often involve percentage-based discounts. Calculating the final price after a discount requires accurate percentage calculation.
- Analyzing financial statements: Financial reports, such as income statements and balance sheets, utilize percentages to represent various ratios and proportions, crucial for financial analysis and decision-making.
- Tax calculations: Sales tax, income tax, and other taxes are frequently expressed as percentages of the total amount.
2. Shopping and Retail:
- Comparing prices: Percentage calculations are essential when comparing prices and determining the best deals, especially when considering discounts and sales tax.
- Calculating tips: Calculating a gratuity or tip at a restaurant often involves a percentage of the total bill.
- Understanding markups: Businesses use percentage markups to determine the selling price of their products or services, considering their costs and desired profit margins.
3. Everyday Life:
- Recipe adjustments: Scaling recipes up or down often involves adjusting ingredient quantities using percentages.
- Understanding statistics: Many statistical data and reports utilize percentages to represent proportions and trends, facilitating interpretation and analysis.
- Calculating grades: In education, grades are frequently expressed as percentages, reflecting a student's performance relative to the total possible score.
4. Scientific and Engineering Applications:
- Determining efficiency: In various scientific and engineering contexts, percentages are used to represent efficiency, effectiveness, and accuracy.
- Analyzing data: Scientific experiments and data analysis frequently involve the use of percentages to represent proportions and trends in experimental results.
Mastering Percentage Calculations: Tips and Tricks
While percentage calculations are fundamentally straightforward, mastering them requires consistent practice and a deep understanding of the underlying concepts. Here are some tips and tricks to improve your proficiency:
- Practice regularly: The key to mastering any skill is consistent practice. Work through various percentage problems, starting with simple ones and gradually progressing to more complex scenarios.
- Use different methods: Familiarize yourself with different methods for calculating percentages, such as decimal conversion, fraction conversion, and proportion. This allows you to choose the most efficient approach depending on the specific problem.
- Understand the concepts: Ensure you have a solid grasp of the fundamental concepts related to percentages, including converting percentages to decimals and fractions.
- Utilize online resources: Numerous online resources, including calculators, tutorials, and practice problems, can help you improve your understanding and skills.
- Break down complex problems: If you encounter a complex percentage problem, break it down into smaller, more manageable steps. This will make the problem less daunting and increase your chances of arriving at the correct answer.
- Check your work: Always double-check your answers to ensure accuracy. Using a different method to solve the same problem can help verify your results.
Beyond the Basics: More Complex Percentage Problems
While the initial problem was straightforward, percentage calculations can become more complex. Consider these examples:
- Calculating percentage increase or decrease: This involves finding the percentage change between two values.
- Calculating percentage points: Percentage points represent the absolute difference between two percentages, not a percentage change.
- Compound interest: This involves calculating interest on both the principal amount and accumulated interest.
Mastering these advanced percentage calculations requires a deeper understanding of mathematical principles and careful attention to detail. However, the foundation laid by understanding simple percentage problems like "What is 20% of 10 dollars?" provides a strong base for tackling more complex challenges.
Conclusion
The seemingly simple question, "What is 20% of 10 dollars?" serves as a springboard to understanding the significant role percentages play in our daily lives. From managing personal finances to understanding complex scientific data, proficiency in percentage calculations is a valuable skill with far-reaching applications. By mastering the basic concepts and practicing regularly, you can confidently tackle a wide range of percentage-related problems and enhance your ability to analyze and interpret quantitative information effectively. Remember, consistent practice and a strong understanding of fundamental principles are the keys to mastering percentages and unlocking their practical potential.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 20 Of 10 Dollars . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.