What Is 20 Out Of 30 As A Percentage
News Co
May 02, 2025 · 5 min read
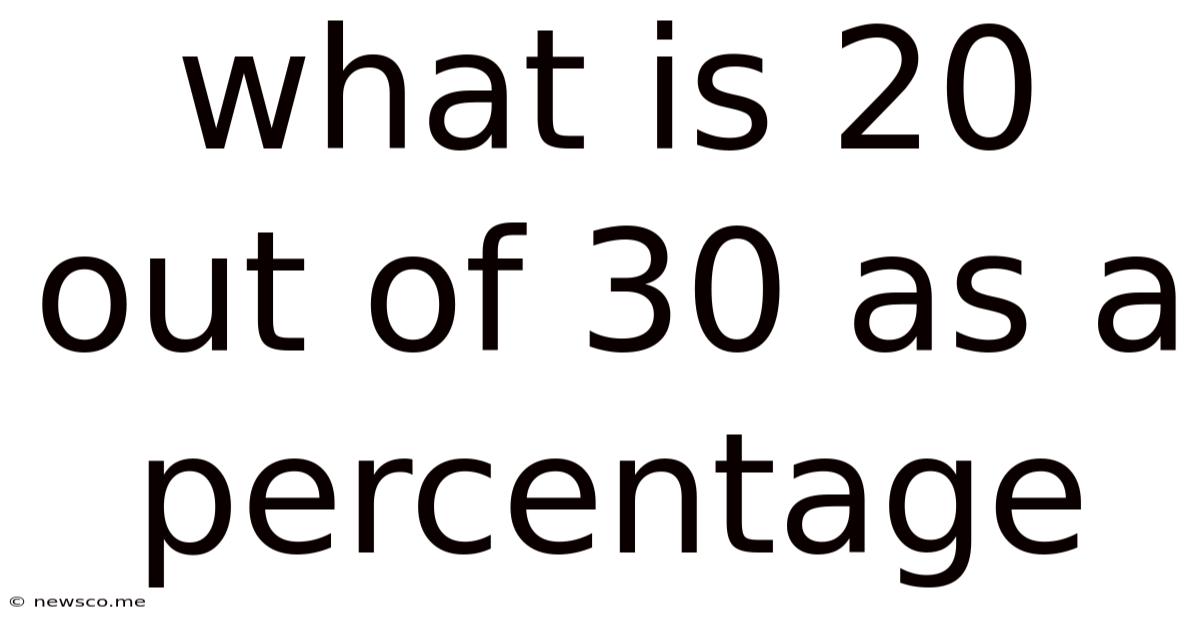
Table of Contents
What is 20 out of 30 as a Percentage? A Comprehensive Guide
Calculating percentages is a fundamental skill applicable across numerous areas of life, from academic assessments to financial planning and everyday decision-making. Understanding how to convert fractions into percentages is crucial for interpreting data, comparing values, and making informed choices. This comprehensive guide will delve into the process of determining what 20 out of 30 represents as a percentage, providing a step-by-step explanation and exploring various methods to achieve the solution. We'll also look at broader applications and contextual understanding of percentages.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" is derived from the Latin "per centum," meaning "out of a hundred." Percentages are denoted by the symbol "%". For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Calculating 20 out of 30 as a Percentage: The Basic Method
The most straightforward method to determine the percentage involves three simple steps:
1. Form a Fraction: Express the given numbers as a fraction. In this case, 20 out of 30 is written as 20/30.
2. Convert the Fraction to a Decimal: Divide the numerator (the top number) by the denominator (the bottom number). 20 divided by 30 equals 0.666666... (a recurring decimal).
3. Convert the Decimal to a Percentage: Multiply the decimal by 100 and add the "%" symbol. 0.666666... multiplied by 100 equals 66.6666...%.
Therefore, 20 out of 30 is 66.67% (rounded to two decimal places).
Alternative Methods for Percentage Calculation
While the basic method is effective, alternative approaches can be equally useful, especially when dealing with more complex scenarios or mental calculations.
Method 1: Simplification of Fractions:
Before converting to a decimal, simplify the fraction 20/30 by finding the greatest common divisor (GCD) of both numbers. The GCD of 20 and 30 is 10. Dividing both the numerator and the denominator by 10 simplifies the fraction to 2/3.
Now, convert 2/3 to a decimal: 2 divided by 3 is approximately 0.6667.
Multiply by 100 to obtain the percentage: 0.6667 x 100 = 66.67%
This method reduces the complexity of the division, making it easier to perform calculations, especially without a calculator.
Method 2: Using Proportions:
A proportion is an equation stating that two ratios are equal. We can set up a proportion to solve this problem:
20/30 = x/100
To solve for 'x' (the percentage), cross-multiply:
30x = 2000
x = 2000/30
x ≈ 66.67
Therefore, 20 out of 30 is approximately 66.67%.
This method is particularly helpful when comparing different ratios or scaling up values.
Practical Applications of Percentage Calculations
Understanding percentage calculations has broad implications across various aspects of life:
1. Academic Performance:
Calculating grades, assessing test scores, and understanding overall academic progress often involve percentage calculations. A score of 20 out of 30 on a test indicates a performance level of 66.67%, providing a clear measure of achievement.
2. Financial Management:
Percentages are vital in understanding interest rates, discounts, tax calculations, profit margins, and investment returns. Calculating percentage increases or decreases in financial figures is crucial for budgeting, saving, and investing effectively.
3. Business and Economics:
Analyzing market share, sales growth, economic indicators, and inflation rates all depend heavily on percentage calculations. Understanding percentages enables businesses to make data-driven decisions and track performance effectively.
4. Everyday Life:
Calculating tips at restaurants, determining sale discounts in stores, and understanding nutritional information on food labels all utilize percentage calculations. These skills empower informed consumer decisions.
5. Science and Research:
Many scientific calculations and experimental data analyses involve percentages, such as expressing the concentration of solutions, analyzing statistical data, and presenting research findings.
Beyond the Basics: Understanding Percentage Change
While calculating a percentage from a fraction is fundamental, understanding percentage change is equally important. Percentage change measures the relative difference between two values over time or across different scenarios. It is calculated using the formula:
[(New Value - Old Value) / Old Value] x 100%
For example, if a value increases from 20 to 30, the percentage change is:
[(30 - 20) / 20] x 100% = 50%
This indicates a 50% increase. Similarly, if the value decreases from 30 to 20, the percentage change would be a -33.33% decrease.
Common Mistakes to Avoid
When calculating percentages, several common mistakes can lead to inaccuracies:
-
Incorrect Fraction Formation: Ensuring the correct numerator and denominator are used in the initial fraction is crucial. Misplacing these values will result in an incorrect percentage.
-
Rounding Errors: Rounding off decimal values too early in the calculation can lead to accumulating errors, affecting the final percentage. It's best to round only at the final stage.
-
Misunderstanding Percentage Change: Failing to distinguish between calculating a simple percentage and calculating percentage change can lead to incorrect interpretations.
-
Incorrect use of calculators: Ensure your calculator is being used correctly, especially with the order of operations. Incorrect input can significantly affect the result.
Conclusion: Mastering Percentage Calculations
The ability to calculate percentages is a fundamental life skill with broad applications. Understanding the basic methods, exploring alternative approaches, and being mindful of common mistakes will empower you to accurately determine percentages in various contexts. From assessing academic performance to managing finances and making informed everyday decisions, a solid grasp of percentage calculations is essential for navigating the quantitative aspects of our world. By applying the principles outlined in this guide, you can confidently tackle percentage problems and effectively interpret quantitative information. Remember to practice regularly to solidify your understanding and build confidence in your calculations.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 20 Out Of 30 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.