What Is 20 Percent Of 300
News Co
Mar 20, 2025 · 4 min read
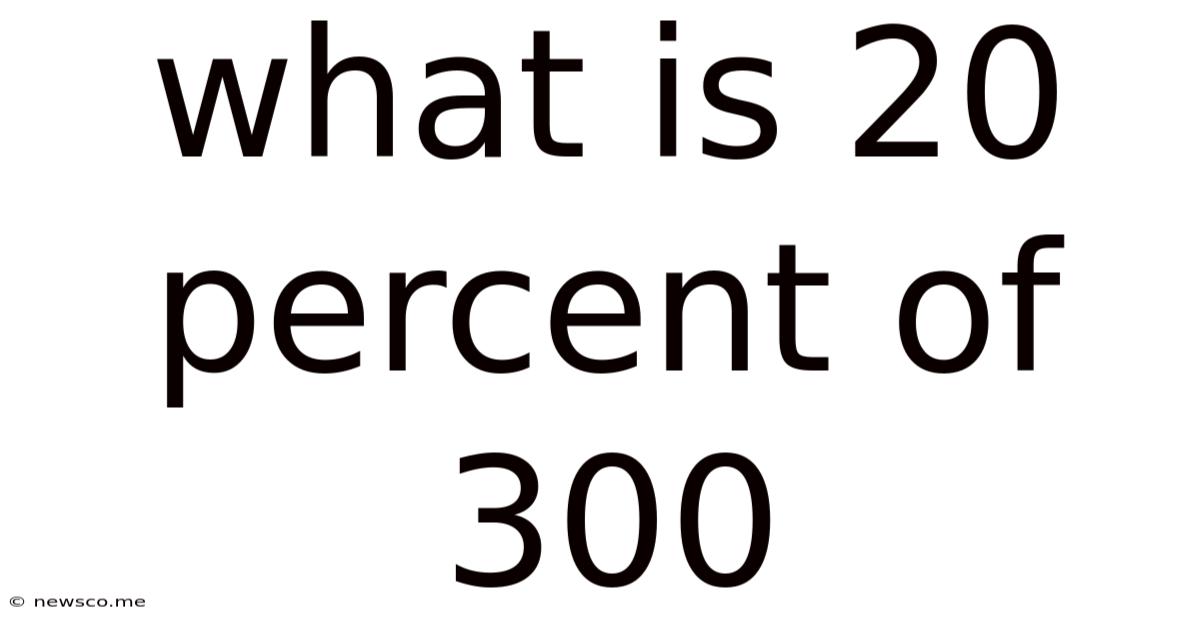
Table of Contents
What is 20 Percent of 300? A Deep Dive into Percentage Calculations
Finding 20 percent of 300 might seem like a simple task, readily solvable with a calculator. However, understanding the underlying principles of percentage calculations is crucial for various applications, from everyday budgeting to complex financial analysis. This article delves deep into the calculation of 20% of 300, exploring multiple methods, providing practical examples, and explaining the broader context of percentage calculations.
Understanding Percentages
Before we tackle the specific problem, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred." Therefore, 20% means 20 out of 100, or 20/100, which simplifies to 1/5.
This fundamental understanding is vital for solving any percentage problem. We can express percentages as decimals or fractions, providing flexibility in our calculations.
Method 1: Using the Decimal Conversion
The most common and arguably easiest method to calculate 20% of 300 involves converting the percentage to a decimal. To do this, we divide the percentage by 100:
20% ÷ 100 = 0.20
Now, we simply multiply this decimal by the number we're interested in:
0.20 x 300 = 60
Therefore, 20% of 300 is 60.
This method is straightforward and works efficiently for most percentage calculations.
Method 2: Using Fractions
As mentioned earlier, 20% can be expressed as the fraction 1/5. This allows us to solve the problem using fraction multiplication:
(1/5) x 300 = 300/5 = 60
Again, we arrive at the answer: 20% of 300 is 60. This method highlights the interchangeable nature of decimals and fractions in percentage calculations. It's particularly useful when dealing with percentages that have easy fractional equivalents (like 25%, 50%, 75%).
Method 3: Using Proportions
Percentage problems can also be solved using proportions. We set up a proportion where we relate the percentage to the whole and the unknown part to the total number:
20/100 = x/300
To solve for x (which represents 20% of 300), we cross-multiply:
20 * 300 = 100 * x
6000 = 100x
x = 6000/100
x = 60
Once again, we confirm that 20% of 300 is 60. The proportion method emphasizes the relationship between parts and wholes, offering a more conceptual approach to percentage calculations.
Practical Applications: Real-World Examples
Understanding percentage calculations extends far beyond simple mathematical exercises. Let's consider some real-world scenarios where calculating 20% of 300 might be relevant:
1. Sales and Discounts:
Imagine a store offering a 20% discount on a $300 item. The discount amount would be 20% of 300, which is $60. The final price after the discount would be $300 - $60 = $240.
2. Taxes and Commissions:
If a salesperson earns a 20% commission on a $300 sale, their commission would be $60.
3. Tip Calculation:
In some cultures, a 20% tip is considered standard. On a $300 restaurant bill, a 20% tip would amount to $60.
4. Financial Analysis:
In finance, percentages are used extensively. Calculating a 20% return on a $300 investment, for example, involves similar calculations.
5. Data Analysis and Statistics:
Percentages are frequently used to represent proportions and changes in data. For instance, if 20% of 300 survey respondents answered "yes" to a question, it means 60 respondents answered affirmatively.
Beyond the Basics: More Complex Percentage Problems
While calculating 20% of 300 is a straightforward example, many real-world applications involve more complex percentage problems. These might involve:
- Calculating the percentage increase or decrease: For example, finding the percentage increase from 300 to 360.
- Finding the original amount given a percentage and a resulting amount: For instance, if an item is on sale for $240 after a 20% discount, what was the original price?
- Working with multiple percentages: Calculating successive discounts or markups.
These scenarios often require a deeper understanding of percentage principles and may necessitate the use of algebraic equations or more advanced mathematical techniques. However, the fundamental principles discussed earlier still form the foundation for solving these more complex problems.
Mastering Percentages: Tips and Tricks
To become proficient in percentage calculations, consider these helpful tips:
- Practice regularly: The more you practice, the more comfortable you'll become with the different methods.
- Understand the underlying concepts: Focus on the relationship between percentages, decimals, and fractions.
- Use multiple methods: Try solving the same problem using different approaches to strengthen your understanding.
- Utilize online calculators and resources: These can be helpful for checking your work and exploring more advanced problems.
- Break down complex problems: Divide larger problems into smaller, more manageable steps.
Conclusion
Calculating 20% of 300, while seemingly simple, provides a solid entry point into the world of percentage calculations. Mastering this fundamental skill opens doors to tackling more complex problems in various fields, from everyday budgeting to sophisticated financial modeling. By understanding the different methods—decimal conversion, fraction use, and proportions—and practicing regularly, you'll build a strong foundation in percentage calculations, empowering you to confidently handle numerical challenges in your personal and professional life. Remember, practice makes perfect, and with consistent effort, you'll become adept at navigating the world of percentages.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 20 Percent Of 300 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.