What Is 22/15 As A Mixed Number
News Co
May 08, 2025 · 5 min read
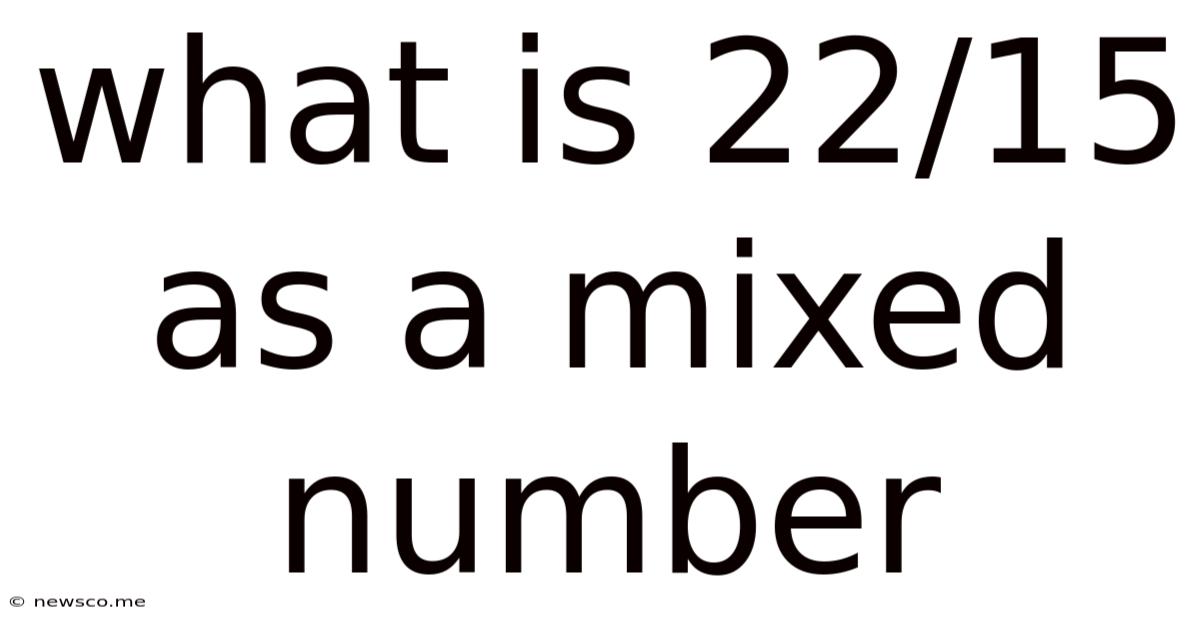
Table of Contents
What is 22/15 as a Mixed Number? A Comprehensive Guide
The question, "What is 22/15 as a mixed number?" might seem simple at first glance, but it opens the door to a deeper understanding of fractions and their various representations. This comprehensive guide will not only answer this specific question but also explore the underlying concepts, providing you with the tools to convert any improper fraction into a mixed number with confidence. We'll delve into the practical applications and even touch upon the historical context of these mathematical representations.
Understanding Fractions: A Quick Refresher
Before we tackle the conversion of 22/15, let's briefly review the fundamental components of a fraction. A fraction represents a part of a whole. It consists of two main parts:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
Fractions can be categorized into two types:
- Proper Fractions: The numerator is smaller than the denominator (e.g., 1/2, 3/4). These fractions represent a value less than one.
- Improper Fractions: The numerator is greater than or equal to the denominator (e.g., 7/4, 5/5). These fractions represent a value greater than or equal to one. Our focus today is on improper fractions, specifically 22/15.
Converting Improper Fractions to Mixed Numbers
A mixed number combines a whole number and a proper fraction. It's a more intuitive way to represent improper fractions, particularly when dealing with real-world applications. The process of conversion involves dividing the numerator by the denominator.
Step-by-step conversion of 22/15:
-
Divide the numerator by the denominator: Divide 22 by 15. This gives us a quotient of 1 and a remainder of 7.
-
The quotient becomes the whole number: The quotient, 1, forms the whole number part of our mixed number.
-
The remainder becomes the numerator of the proper fraction: The remainder, 7, becomes the numerator of the proper fraction.
-
The denominator remains the same: The denominator of the proper fraction remains the same as the original fraction's denominator, which is 15.
Therefore, 22/15 as a mixed number is 1 7/15.
Visualizing the Conversion: A Real-World Analogy
Imagine you have 22 slices of pizza, and each pizza has 15 slices. How many whole pizzas do you have, and how many slices are left over?
You can make one complete pizza (15 slices) and have 7 slices remaining. This corresponds directly to our mixed number, 1 7/15. This visual representation helps to solidify the concept of converting improper fractions to mixed numbers.
Why Use Mixed Numbers?
While improper fractions are perfectly valid representations, mixed numbers often provide a clearer and more practical understanding, especially in everyday contexts. For instance, if you're measuring ingredients for a recipe, saying you need "1 7/15 cups of flour" is significantly easier to comprehend than "22/15 cups of flour."
Mixed numbers enhance communication and comprehension in various situations. They are particularly useful in:
- Measurement: Representing quantities that exceed a whole unit.
- Cooking and Baking: Precisely measuring ingredients.
- Construction and Engineering: Working with dimensions and materials.
- Everyday Life: Understanding parts of wholes in a relatable manner.
Beyond 22/15: Mastering the Conversion Process
The process of converting improper fractions to mixed numbers is applicable to any improper fraction. Let's consider a few examples:
- 17/5: 17 divided by 5 is 3 with a remainder of 2. Therefore, 17/5 = 3 2/5.
- 29/8: 29 divided by 8 is 3 with a remainder of 5. Therefore, 29/8 = 3 5/8.
- 45/12: 45 divided by 12 is 3 with a remainder of 9. Therefore, 45/12 = 3 9/12 (which can be simplified to 3 ¾).
Simplifying Fractions: A Crucial Step
In some cases, the resulting proper fraction in the mixed number can be simplified. This means reducing the fraction to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD).
For example, in the case of 45/12, we got 3 9/12. Both 9 and 12 are divisible by 3. Simplifying the fraction, we get 3 ¾. Always check for simplification opportunities to represent your answer in its most concise form.
The Historical Context of Fractions and Mixed Numbers
The use of fractions and mixed numbers dates back to ancient civilizations. Evidence suggests that Egyptians used fractions as early as 1650 BC, although their system differed from the one we use today. The Babylonians also developed sophisticated methods for working with fractions, albeit using a sexagesimal (base-60) system. The modern notation, with the numerator above the denominator and a horizontal line separating them, evolved over centuries. The use of mixed numbers provided a way to express quantities more naturally and efficiently in many practical situations.
Advanced Applications and Extensions
The concepts explored here form the foundation for more advanced mathematical operations. Understanding improper fractions and their mixed number equivalents is crucial for:
- Algebra: Solving equations and simplifying expressions involving fractions.
- Calculus: Working with limits, derivatives, and integrals.
- Geometry: Calculating areas, volumes, and other geometric properties.
Conclusion: Mastering Fractions for Real-World Success
Converting 22/15 to a mixed number, resulting in 1 7/15, is a simple yet fundamental step in mastering the world of fractions. This seemingly small task opens the door to a deeper understanding of mathematical representation and empowers you to tackle more complex problems with confidence. By grasping the underlying principles and practicing conversion techniques, you'll improve your mathematical skills and equip yourself with valuable tools for various real-world applications. Remember to always check for simplification opportunities to express your answers in their most concise and elegant form. The journey into the world of fractions is rewarding and beneficial, both mathematically and practically. So, embrace the challenge, practice regularly, and unlock the power of fractions!
Latest Posts
Latest Posts
-
How Many Whole Numbers Are Less Than N
May 08, 2025
-
Lateral Surface Area Of A Hexagonal Pyramid
May 08, 2025
-
Find The Area Of The Trapezoid Shown Below
May 08, 2025
-
Find The Inverse Of The Given Matrix If It Exists
May 08, 2025
-
What Is 30 Percent Off 20 Dollars
May 08, 2025
Related Post
Thank you for visiting our website which covers about What Is 22/15 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.