What Is 25 Percent Of 200
News Co
Apr 01, 2025 · 5 min read
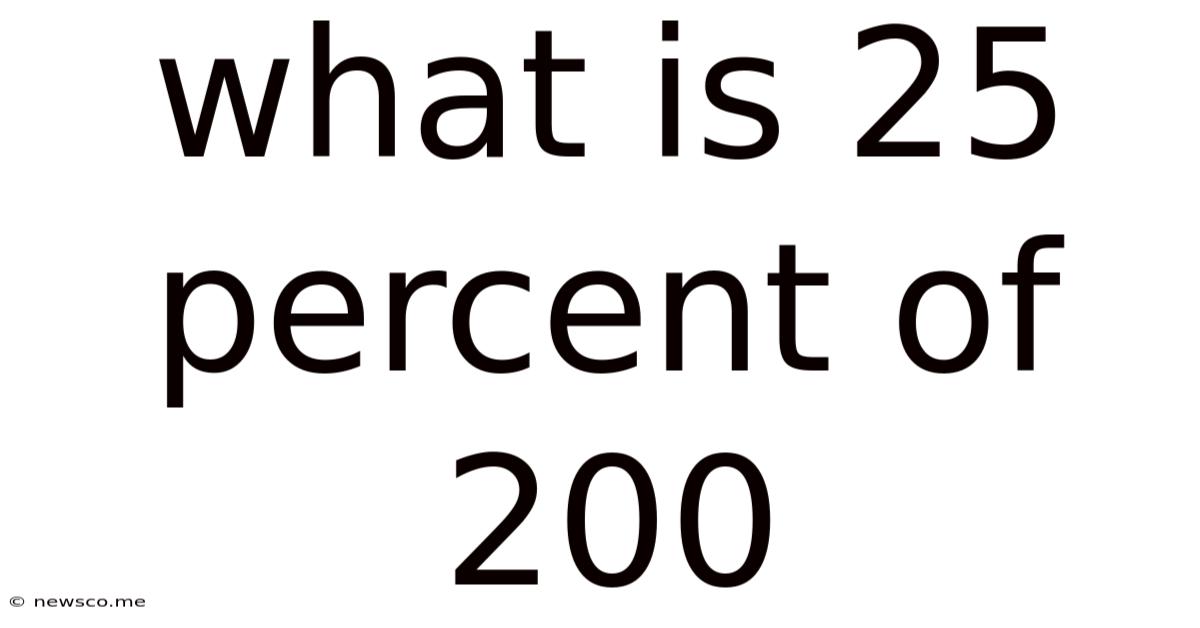
Table of Contents
What is 25 Percent of 200? A Deep Dive into Percentages and Their Applications
The seemingly simple question, "What is 25 percent of 200?" opens a door to a vast world of mathematical concepts and practical applications. While the answer itself is straightforward (50), understanding the underlying principles and exploring various methods to solve this problem unlocks a deeper understanding of percentages, their importance in everyday life, and their role in more complex calculations. This comprehensive guide will not only provide the solution but delve into the "why" and "how," exploring different approaches and showcasing real-world scenarios where such calculations are vital.
Understanding Percentages: The Foundation
Before tackling the problem directly, let's establish a solid understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The term "percent" originates from the Latin "per centum," meaning "out of one hundred." Therefore, 25 percent (25%) means 25 out of 100, which can be represented as the fraction 25/100 or the decimal 0.25. This fundamental understanding is crucial for solving percentage problems.
Method 1: The Fraction Method
This is perhaps the most intuitive method for calculating percentages. We can rephrase the problem as: "What is 25/100 of 200?"
-
Convert the percentage to a fraction: 25% = 25/100
-
Multiply the fraction by the whole number: (25/100) * 200
-
Simplify the equation: Notice that 200 can be divided by 100, simplifying the calculation to 25 * 2.
-
Calculate the result: 25 * 2 = 50
Therefore, 25% of 200 is 50.
Method 2: The Decimal Method
This method involves converting the percentage to a decimal and then multiplying.
-
Convert the percentage to a decimal: 25% = 0.25 (simply divide the percentage by 100)
-
Multiply the decimal by the whole number: 0.25 * 200
-
Calculate the result: 0.25 * 200 = 50
This method is often preferred for its efficiency, especially when dealing with more complex calculations or using calculators.
Method 3: Using Proportions
This method uses the concept of ratios and proportions to solve the problem. We can set up a proportion:
- 25/100 = x/200
Where 'x' represents the unknown value (25% of 200). To solve for x, we cross-multiply:
-
25 * 200 = 100 * x
-
5000 = 100x
-
x = 5000 / 100
-
x = 50
This method reinforces the fundamental relationship between percentages and proportions and is particularly useful for understanding the underlying mathematical principles.
Real-World Applications: Where Percentages Matter
Understanding percentage calculations is essential in numerous real-world scenarios. Here are just a few examples:
-
Sales and Discounts: Calculating discounts offered during sales is a common application of percentages. If a store offers a 25% discount on a $200 item, the discount amount is $50 (25% of $200), and the final price is $150.
-
Taxes and Interest: Calculating taxes on purchases or interest on loans involves percentage calculations. Understanding these calculations helps in managing personal finances effectively.
-
Profit Margins and Markups: Businesses use percentages to determine profit margins and markups on products. Calculating the percentage profit on a sale is crucial for assessing business performance.
-
Statistics and Data Analysis: Percentages are fundamental in presenting and interpreting data in various fields, including science, economics, and social sciences. Understanding percentages allows for effective data visualization and analysis.
-
Surveys and Polls: Percentages are used extensively to represent results from surveys and polls, enabling meaningful interpretations of public opinion and trends.
-
Financial Investments: Calculating returns on investments, understanding interest rates, and analyzing investment performance all rely heavily on percentage calculations.
Beyond the Basics: More Complex Percentage Problems
While the example of finding 25% of 200 is relatively simple, the principles extend to more complex scenarios:
-
Finding the Percentage: Instead of finding a percentage of a number, you might need to find what percentage one number is of another. For example, "What percentage of 200 is 50?" This requires dividing 50 by 200 and multiplying by 100 to get 25%.
-
Finding the Original Number: You might know the percentage and the resulting value and need to find the original number. For example, "50 is 25% of what number?" This involves setting up an equation and solving for the unknown variable.
-
Compound Interest: Compound interest calculations involve applying percentages repeatedly over time. This requires understanding exponential growth and decay principles.
-
Percentage Increase and Decrease: Calculating percentage increase or decrease involves comparing two values and expressing the change as a percentage of the original value.
Mastering Percentages: Tips and Practice
Mastering percentage calculations requires consistent practice. Here are some tips to improve your skills:
-
Practice Regularly: Solve various percentage problems regularly to build fluency and confidence.
-
Use Different Methods: Experiment with different methods (fraction, decimal, proportion) to find the approach that best suits your understanding.
-
Break Down Complex Problems: Break down complex percentage problems into smaller, manageable steps.
-
Use Online Resources: Utilize online calculators and tutorials to check your answers and reinforce your understanding.
-
Relate to Real-World Scenarios: Apply percentage calculations to real-life situations to make the learning process more engaging and relevant.
In conclusion, while the answer to "What is 25 percent of 200?" is simply 50, the underlying concepts and applications of percentages extend far beyond this basic calculation. Understanding percentages is a fundamental skill with widespread applications across various fields. By mastering these principles and practicing regularly, you can confidently tackle more complex percentage problems and use this knowledge to solve practical problems in your daily life.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 25 Percent Of 200 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.