What Is 25 Percent Of 50
News Co
Mar 19, 2025 · 6 min read
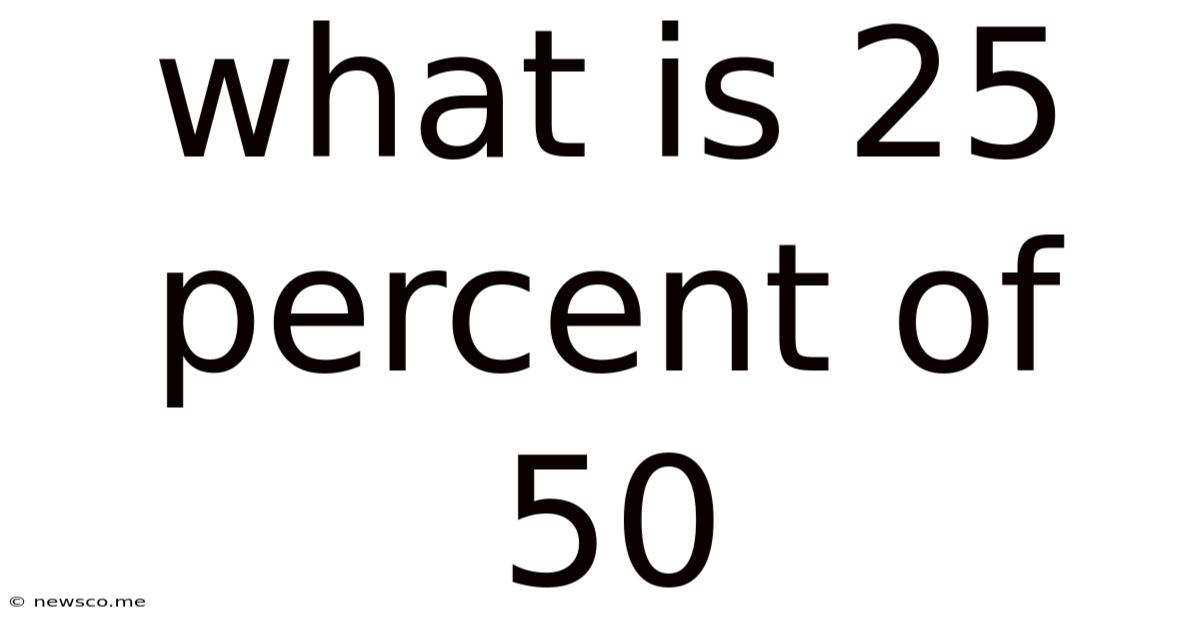
Table of Contents
What is 25 Percent of 50? A Deep Dive into Percentages and Their Applications
Finding 25% of 50 might seem like a simple calculation, but understanding the underlying principles of percentages unlocks a world of practical applications in various fields. This article delves into the intricacies of percentage calculations, explores multiple methods for solving this specific problem, and showcases real-world examples where understanding percentages is crucial. We'll also touch upon the importance of percentages in various professional fields and how mastering them can enhance your problem-solving skills.
Understanding Percentages: The Basics
A percentage is simply a fraction expressed as a part of 100. The term "percent" literally means "per hundred" (from the Latin "per centum"). So, 25% means 25 out of 100, or 25/100. This can be further simplified to 1/4. This fundamental understanding is key to solving percentage problems.
Key Concepts:
- The Whole: This is the total amount you're considering. In our example, the whole is 50.
- The Part: This is the portion of the whole that represents the percentage. We need to find the part that represents 25% of 50.
- The Percentage: This is the rate expressed as a number followed by the "%" symbol, indicating the proportion of the whole. In our case, the percentage is 25%.
Calculating 25% of 50: Three Effective Methods
There are several ways to calculate 25% of 50. Let's explore three common and effective approaches:
Method 1: Using the Fraction Method
Since 25% is equivalent to 1/4, we can simply divide 50 by 4:
50 / 4 = 12.5
Therefore, 25% of 50 is 12.5.
This method is particularly useful when dealing with simple percentages that have easy-to-handle fraction equivalents, like 25%, 50%, and 75%.
Method 2: Using Decimal Conversion
We can convert the percentage to a decimal by dividing it by 100. 25% divided by 100 is 0.25. Then, multiply this decimal by the whole number (50):
0.25 * 50 = 12.5
This method is more versatile and works well for any percentage, not just those with simple fraction equivalents. It's a widely used approach for percentage calculations.
Method 3: Using Proportions
This method uses the concept of ratios to solve for the unknown part. We can set up a proportion:
25/100 = x/50
Where 'x' represents the unknown part (25% of 50). To solve for x, we cross-multiply:
25 * 50 = 100 * x
1250 = 100x
x = 1250 / 100
x = 12.5
Again, we find that 25% of 50 is 12.5. This method is valuable for understanding the underlying relationship between percentages and proportions, making it a useful tool for more complex problems.
Real-World Applications of Percentage Calculations
Understanding percentages is essential in various aspects of daily life and professional fields. Let's explore some real-world scenarios where this knowledge proves invaluable:
1. Retail and Sales:
- Discounts: Stores frequently advertise discounts as percentages. Knowing how to calculate percentages quickly allows you to determine the actual price after a discount. For example, a 25% discount on a $50 item results in a savings of $12.50 (as we calculated above).
- Sales Tax: Sales tax is added to the price of goods and services as a percentage. Understanding how to calculate sales tax helps you determine the final cost of a purchase.
- Profit Margins: Businesses rely on percentage calculations to determine their profit margins, analyzing the difference between the cost price and selling price of goods.
2. Finance and Investment:
- Interest Rates: Interest on loans, savings accounts, and investments is usually expressed as a percentage. Understanding these percentages helps in making informed financial decisions.
- Investment Returns: Tracking investment returns involves percentage calculations to assess the growth or decline of investments over time.
- Compound Interest: The calculation of compound interest is entirely dependent on understanding and applying percentage calculations.
3. Statistics and Data Analysis:
- Data Representation: Percentages are widely used to represent data in charts, graphs, and reports, making it easier to visualize and interpret information.
- Probability: Probability is often expressed as a percentage, providing a measure of the likelihood of an event occurring.
- Surveys and Polls: Survey results and polls often use percentages to summarize responses and draw conclusions.
4. Everyday Life:
- Tipping: Calculating a tip in a restaurant often involves determining a certain percentage of the bill.
- Recipe Scaling: Scaling up or down recipes requires adjustments to ingredients, often using percentage calculations to maintain proportions.
- Comparisons: Percentages allow for convenient comparison of different values, even if the underlying quantities are drastically different. For example, comparing the percentage increase in sales across different stores.
Beyond the Basics: More Complex Percentage Problems
While 25% of 50 is a straightforward calculation, the principles involved can be applied to much more complex problems. For instance:
- Finding the Percentage: Instead of finding the part, you might need to determine what percentage one number represents of another. For example, what percentage is 15 of 60?
- Finding the Whole: You might know the part and the percentage and need to find the whole. For example, if 20% of a number is 10, what is the number?
- Multiple Percentages: Problems might involve calculating multiple percentages sequentially, such as calculating sales tax on a discounted item.
- Percentage Change: This involves calculating the percentage increase or decrease between two values. This is very commonly used in finance and business.
Mastering these more advanced percentage calculations requires a solid understanding of the fundamental principles discussed earlier, including the ability to manipulate equations and solve for unknown variables.
Improving Your Percentage Calculation Skills
Practice is crucial to becoming proficient in percentage calculations. Here are some tips to enhance your skills:
- Regular Practice: Solve various percentage problems regularly, starting with simple examples and gradually increasing the complexity.
- Utilize Different Methods: Experiment with different methods to solve problems, choosing the most efficient approach depending on the context.
- Check Your Work: Always verify your answers using a different method or a calculator to ensure accuracy.
- Real-World Application: Apply percentage calculations to real-life scenarios to strengthen your understanding and improve retention.
- Online Resources: Utilize online resources, such as educational websites and calculators, to further practice and expand your knowledge.
Conclusion: The Power of Percentages
Understanding percentages is a fundamental skill with far-reaching applications across numerous fields. While finding 25% of 50 might seem trivial, the underlying principles are far-reaching. Mastering percentage calculations improves your problem-solving skills, enables you to make informed decisions, and enhances your understanding of data and information in various contexts. From managing personal finances to analyzing complex business data, the ability to accurately and quickly calculate percentages is an invaluable asset. By consistently practicing and applying these skills, you'll find yourself more confident and capable in a vast array of situations.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 25 Percent Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.