What Is 3 10 As A Percentage
News Co
Apr 06, 2025 · 4 min read
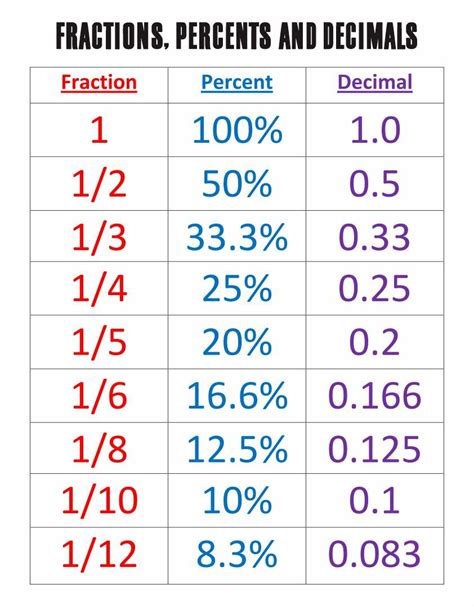
Table of Contents
What is 3/10 as a Percentage? A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and tips to understanding statistics and financial data. This comprehensive guide will not only answer the question, "What is 3/10 as a percentage?" but also delve deep into the underlying principles, offering various methods to solve similar problems and providing practical examples to solidify your understanding.
Understanding Fractions and Percentages
Before diving into the specific calculation, let's clarify the concepts of fractions and percentages.
Fractions: A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts you have, and the denominator indicates the total number of equal parts the whole is divided into. For example, in the fraction 3/10, 3 is the numerator and 10 is the denominator. This means we have 3 parts out of a total of 10 equal parts.
Percentages: A percentage is a way of expressing a fraction or a decimal as a portion of 100. The symbol "%" is used to represent percentage. Essentially, a percentage indicates how many parts per hundred. For instance, 50% means 50 parts out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Converting 3/10 to a Percentage: The Methods
There are several ways to convert the fraction 3/10 into a percentage. Let's explore the most common methods:
Method 1: Using the Conversion Formula
The most straightforward approach involves using the basic conversion formula:
(Fraction × 100)% = Percentage
In our case:
(3/10 × 100)% = 30%
Therefore, 3/10 is equal to 30%.
Method 2: Converting the Fraction to a Decimal
Another method involves first converting the fraction to a decimal and then multiplying by 100 to get the percentage. To convert a fraction to a decimal, simply divide the numerator by the denominator:
3 ÷ 10 = 0.3
Now, multiply the decimal by 100:
0.3 × 100 = 30
Therefore, 3/10 as a decimal is 0.3, which is equivalent to 30%.
Method 3: Understanding the Relationship Between Fractions and Percentages
Understanding the relationship between fractions and percentages intuitively can be helpful. Since a percentage is always out of 100, consider what fraction of 100 is equivalent to 3/10. We can set up a proportion:
3/10 = x/100
To solve for x, we can cross-multiply:
10x = 300
x = 30
Therefore, 3/10 is equal to 30%. This method highlights the proportional relationship between fractions and percentages.
Practical Applications and Examples
The ability to convert fractions to percentages is crucial in many real-world scenarios:
- Calculating Discounts: A store offers a 3/10 discount on an item. This means a 30% discount.
- Determining Test Scores: If you answer 3 out of 10 questions correctly on a quiz, your score is 30%.
- Analyzing Financial Data: Understanding financial reports often involves interpreting fractions and percentages to assess profitability, growth, and risk.
- Understanding Statistics: Statistics frequently use percentages to represent proportions and probabilities. For example, if 3 out of 10 people prefer a particular brand, that represents a 30% preference rate.
- Baking and Cooking: Recipes sometimes use fractions, and understanding their percentage equivalents can help in adjusting recipes.
Beyond 3/10: Mastering Fraction-to-Percentage Conversions
The methods described above can be applied to convert any fraction to a percentage. Let's consider a few more examples:
- 1/4 as a percentage: (1/4 × 100)% = 25%
- 2/5 as a percentage: (2/5 × 100)% = 40%
- 7/8 as a percentage: (7/8 × 100)% = 87.5%
- 5/6 as a percentage: (5/6 × 100)% = 83.33% (approximately)
Dealing with more complex fractions: For fractions with larger numerators and denominators, using a calculator can simplify the process. Remember, the core principle remains the same: divide the numerator by the denominator and then multiply by 100.
Tips and Tricks for Efficient Conversions
- Memorize common fractions and their percentage equivalents: Knowing that 1/2 = 50%, 1/4 = 25%, 1/3 ≈ 33.33%, and 1/5 = 20% can speed up calculations.
- Use a calculator: For more complex fractions, a calculator can help ensure accuracy.
- Practice regularly: The more you practice, the more proficient you will become in converting fractions to percentages.
Conclusion: Mastering the Art of Percentage Conversions
Understanding how to convert fractions to percentages is a valuable skill with far-reaching implications across various aspects of life. By mastering the methods outlined in this guide, you'll be equipped to confidently tackle fraction-to-percentage conversions and apply this knowledge to real-world problems, fostering a deeper understanding of numerical relationships and improving your analytical skills. Remember to practice regularly and utilize the tips and tricks provided to enhance your efficiency and accuracy. The ability to easily convert fractions to percentages will undoubtedly prove to be an asset in your academic pursuits, professional endeavors, and everyday life.
Latest Posts
Latest Posts
-
1 3 Plus 1 3 As A Fraction
Apr 07, 2025
-
What Is The Square Root Of 189
Apr 07, 2025
-
How To Find The Area Of The Shaded Sector
Apr 07, 2025
-
Whats The Square Root Of 78
Apr 07, 2025
-
Whats The Square Root Of 288
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 10 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
