What Is 3 2 Equal To
News Co
Mar 18, 2025 · 5 min read
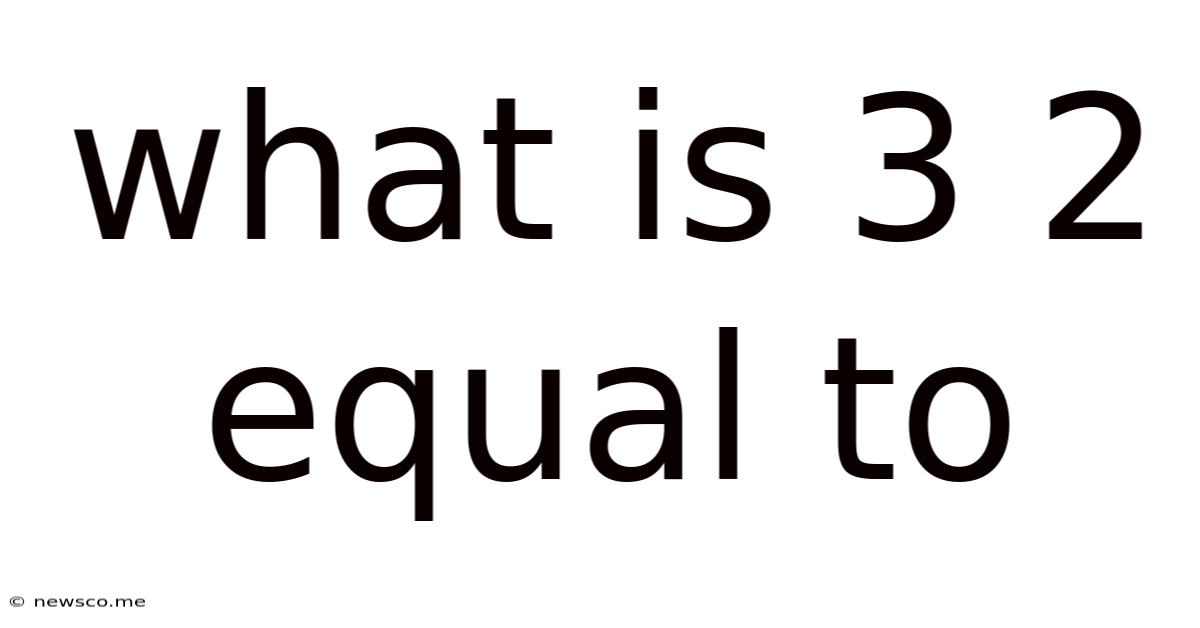
Table of Contents
What is 3 2 Equal To? Exploring the Depths of Mathematical Notation and Interpretation
The seemingly simple question, "What is 3 2 equal to?", opens a fascinating exploration into the nuances of mathematical notation and the importance of clear communication. While the immediate response might be "6," due to the common understanding of multiplication, the absence of an explicit operator introduces ambiguity and highlights the need for precise mathematical language. This article delves into the various interpretations of "3 2," examining different mathematical contexts and exploring the critical role of notation in avoiding confusion.
The Most Likely Interpretation: Implicit Multiplication
In most mathematical contexts, the juxtaposition of two numbers, like "3 2," implies multiplication. This convention is widely used in algebra, programming, and many scientific fields. Therefore, the most straightforward interpretation of "3 2" is:
3 × 2 = 6
This interpretation relies on the implicit multiplication operator, which is understood but not explicitly written. The lack of a visible symbol doesn't change the fundamental operation; it simply relies on a common convention to streamline notation.
Implicit Multiplication in Programming and Scientific Notation
The implicit multiplication convention is particularly prevalent in programming and scientific notation. For instance, in many programming languages, 3*2 and 3 2 would both yield the same result: 6. Similarly, in scientific notation, a number like 2.5 x 10^3 might be written more concisely as 2.5e3 or even 2.5 10^3, with the multiplication implied.
Potential for Ambiguity: The Importance of Clarity
While implicit multiplication is convenient, it can lead to ambiguity, especially in more complex expressions. Consider the expression "3 x 2 + 4". This is clear. Now consider "3 2 + 4". The intended order of operations might not be immediately apparent to everyone. Does it mean (3 × 2) + 4 = 10, or is there a different interpretation?
This ambiguity highlights the importance of explicitly stating mathematical operations to ensure clarity. In situations where ambiguity is possible, it's crucial to use explicit operators (such as the multiplication symbol '×' or the asterisk '*') to remove any doubt.
Beyond Multiplication: Exploring Other Possibilities
While multiplication is the most probable interpretation of "3 2," it's important to consider other, less likely, but mathematically valid possibilities within specific contexts.
Concatenation in String Manipulation
In computer programming, particularly string manipulation, the juxtaposition of numbers could represent concatenation—joining the numbers as strings. In such cases, "3 2" would result in "32". This context-dependent interpretation necessitates an awareness of the data type being handled.
Base-n Number Systems
In different number systems (other than base-10), the meaning of "3 2" could vary. For example, it could be interpreted as a number in base 3, base 2, or even other non-standard bases. However, without explicit indication of the base, such interpretations remain speculative.
Set Theory and Cartesian Products
In set theory, "3 2" might represent a Cartesian product. Given two sets, A with 3 elements and B with 2 elements, their Cartesian product A x B would result in a set containing 6 ordered pairs (3 x 2 = 6). While this is a mathematically valid interpretation, it is highly context-dependent.
Abstract Algebra and Group Theory
In advanced mathematical fields like abstract algebra and group theory, the symbol "3 2" could have entirely different meanings, depending on the specific structure being defined. The interpretation would rely on the axioms and definitions governing the particular mathematical structure.
The Crucial Role of Notation in Mathematics
The ambiguity surrounding "3 2" underscores the pivotal role of precise notation in mathematics. Clear, unambiguous notation is essential for:
-
Avoiding Misunderstandings: Precise notation removes ambiguity and ensures everyone interprets mathematical expressions in the same way.
-
Facilitating Communication: Accurate notation facilitates clear communication of mathematical ideas, both among mathematicians and between mathematicians and non-mathematicians.
-
Enabling Computation: In computing and programming, precise notation is essential for the correct execution of algorithms and calculations.
-
Preventing Errors: Ambiguous notation can lead to errors in calculations, proofs, and implementations.
Best Practices for Mathematical Notation
To avoid ambiguities and ensure clear mathematical communication, consider these best practices:
-
Use Explicit Operators: Always use explicit operators (+, -, ×, ÷) to avoid any confusion about the intended operations.
-
Parentheses for Order of Operations: Use parentheses to explicitly define the order of operations, especially in complex expressions.
-
Specify Base (if applicable): In number systems other than base-10, clearly state the base being used.
-
Contextual Clarity: Ensure that the context of your mathematical expressions is clear and readily understood.
-
Consistency: Maintain consistent notation throughout your mathematical work.
-
Verification: Always verify your interpretation of expressions, especially those that might have multiple potential meanings.
Conclusion: The Power of Precision in Mathematics
The simple question "What is 3 2 equal to?" serves as a powerful reminder of the importance of precise and unambiguous mathematical notation. While the most likely answer is 6, based on the commonly understood convention of implicit multiplication, the potential for ambiguity highlights the need for clarity in mathematical communication. By consistently applying best practices for mathematical notation, we can ensure accurate interpretations, avoid errors, and facilitate clear communication within the field of mathematics and beyond. The power of mathematics lies not only in its results but also in the precision with which those results are expressed and communicated. The seemingly simple "3 2" becomes a powerful example of this principle. Understanding the subtleties of notation is key to mastering mathematics and applying it effectively.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 2 Equal To . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.