What Is 3 4 Divided By 2 3
News Co
Apr 20, 2025 · 5 min read
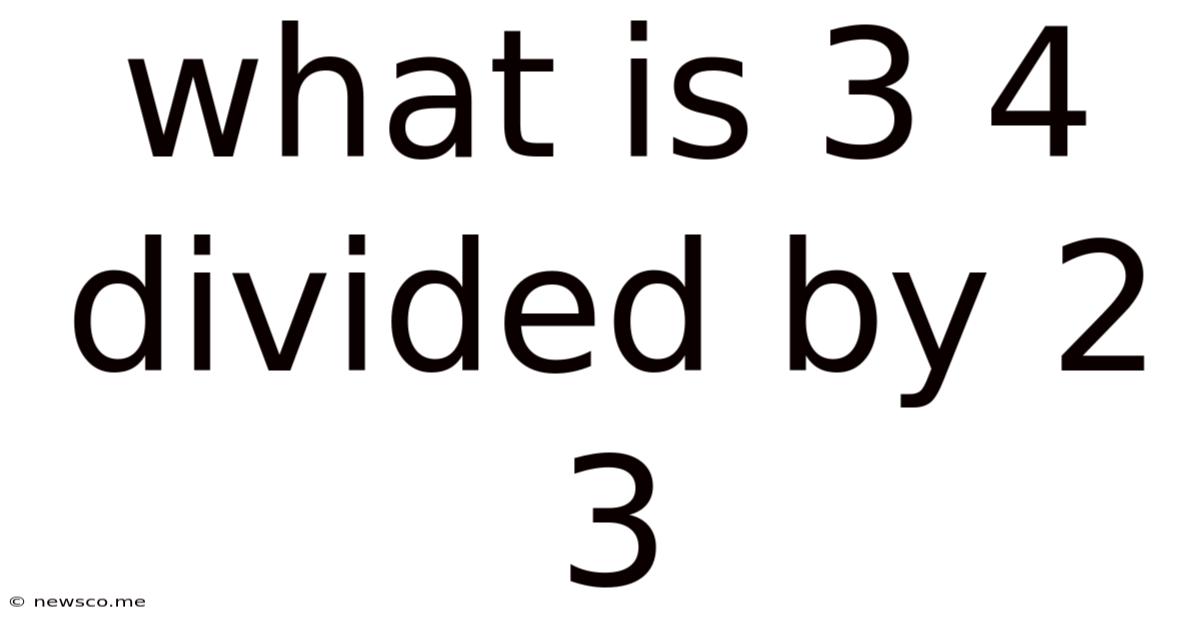
Table of Contents
What is 3/4 Divided by 2/3? A Deep Dive into Fraction Division
The seemingly simple question, "What is 3/4 divided by 2/3?" often trips up students and adults alike. Understanding fraction division is crucial for various mathematical applications, from baking recipes to advanced calculus. This comprehensive guide will not only provide the answer but also explain the why behind the process, equipping you with the skills to confidently tackle similar problems.
Understanding Fraction Division: The "Keep, Change, Flip" Method
The most common method for dividing fractions is the "keep, change, flip" method, also known as the reciprocal method. Let's break it down step-by-step:
1. Keep: Keep the first fraction exactly as it is. In our case, this is 3/4.
2. Change: Change the division sign (÷) to a multiplication sign (×).
3. Flip: Flip (or find the reciprocal of) the second fraction. The reciprocal of 2/3 is 3/2.
Therefore, the problem 3/4 ÷ 2/3 transforms into: 3/4 × 3/2
Performing the Multiplication
Now that we've converted the division problem into a multiplication problem, the process becomes straightforward:
- Multiply the numerators: 3 × 3 = 9
- Multiply the denominators: 4 × 2 = 8
This gives us the answer 9/8.
Converting to a Mixed Number (Optional)
While 9/8 is a perfectly valid answer, it's often preferable to express improper fractions (where the numerator is larger than the denominator) as mixed numbers. To do this:
- Divide the numerator by the denominator: 9 ÷ 8 = 1 with a remainder of 1.
- The whole number part of the result becomes the whole number of the mixed number: This is 1.
- The remainder becomes the numerator of the fraction part, while the denominator remains the same: This gives us 1/8.
Therefore, 9/8 is equivalent to the mixed number 1 1/8. This is the final answer to the problem "What is 3/4 divided by 2/3?".
Visualizing Fraction Division
Understanding the concept becomes easier when visualized. Imagine you have a pizza cut into fourths (3/4 of a pizza). You want to divide this amount into portions that are each 2/3 the size of a whole pizza. How many portions will you get?
The process of division is essentially finding out how many times the second fraction "fits" into the first. The "keep, change, flip" method allows us to mathematically solve this visual puzzle.
Why Does "Keep, Change, Flip" Work?
The "keep, change, flip" method isn't just a trick; it's a consequence of the definition of division. Division is the inverse operation of multiplication. When we divide by a fraction, we're essentially asking, "What do I need to multiply by to get 1?" This is where the reciprocal comes into play.
Let's illustrate this with our example:
3/4 ÷ 2/3 is equivalent to asking: (3/4) x ? = 1
To find the ?, we need to find the reciprocal of 2/3, which is 3/2. Multiplying 3/4 by 3/2 indeed gives us (3/4) x (3/2) = 9/8. If we divide 9/8 (our answer) by 2/3, we will get back our original fraction of 3/4, confirming that the method is mathematically sound.
Expanding on Fraction Division: Real-World Applications
Understanding fraction division isn't merely an academic exercise. It finds practical application in numerous real-world scenarios:
-
Cooking and Baking: Scaling recipes up or down often involves dividing fractional quantities. If a recipe calls for 1/2 cup of flour, and you want to make half the recipe, you'll need to divide 1/2 by 2 (or multiply by 1/2).
-
Sewing and Tailoring: Calculating fabric requirements or adjusting pattern sizes frequently necessitates dividing fractions.
-
Construction and Engineering: Many engineering calculations, especially those involving ratios and proportions, use fraction division.
-
Finance and Investments: Calculating returns on investments, especially when dealing with fractional shares, involves dividing fractions.
-
Data Analysis: When working with datasets where values are expressed as fractions or proportions, division of fractions is frequently necessary.
Tackling More Complex Fraction Division Problems
Once you've mastered the basics, you can tackle more complex problems involving mixed numbers or a series of fraction divisions.
Example 1: Dividing a Mixed Number by a Fraction
Let's say we need to solve 1 1/2 ÷ 1/4.
Step 1: Convert the mixed number to an improper fraction: 1 1/2 = (1 x 2 + 1)/2 = 3/2
Step 2: Apply the "keep, change, flip" method: 3/2 ÷ 1/4 becomes 3/2 x 4/1
Step 3: Multiply: (3 x 4)/(2 x 1) = 12/2 = 6
Example 2: A Chain of Fraction Divisions
Let's solve (1/2 ÷ 1/4) ÷ 1/8.
Step 1: Solve the inner division first: 1/2 ÷ 1/4 = 1/2 x 4/1 = 2
Step 2: Solve the remaining division: 2 ÷ 1/8 = 2 x 8/1 = 16
These examples highlight that the fundamental principles of "keep, change, flip" remain consistent even as the problems become more complex.
Troubleshooting Common Mistakes
Students often encounter a few common pitfalls when dividing fractions:
-
Forgetting to flip the second fraction: This leads to an incorrect multiplication and a wrong answer. Remember the crucial "flip" step!
-
Incorrectly multiplying or simplifying: Double-check your multiplication and simplification to avoid arithmetic errors.
-
Failing to convert mixed numbers to improper fractions before dividing: Mixed numbers must be converted to improper fractions before applying the "keep, change, flip" method.
-
Confusing division with addition or subtraction: Keep a clear distinction between the arithmetic operations.
Mastering Fraction Division: Practice Makes Perfect
The key to mastering fraction division is consistent practice. Start with simple problems and gradually increase the complexity. Work through various examples, and don't hesitate to use visual aids like diagrams or drawings to help you grasp the concept. The more you practice, the more confident and proficient you'll become in solving fraction division problems.
Conclusion: Embracing the Power of Fractions
Fraction division, though initially challenging, becomes manageable with a solid understanding of the underlying principles and consistent practice. The "keep, change, flip" method provides a streamlined approach, while visualizing the process reinforces conceptual understanding. This knowledge equips you to tackle a wide array of mathematical problems in various real-world applications, solidifying your mathematical proficiency and expanding your problem-solving abilities. Remember, practice is key to unlocking the power of fractions and confidently navigating the world of mathematics.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 3 4 Divided By 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.