What Is 3/4 Divided By 2 As A Fraction
News Co
Mar 19, 2025 · 4 min read
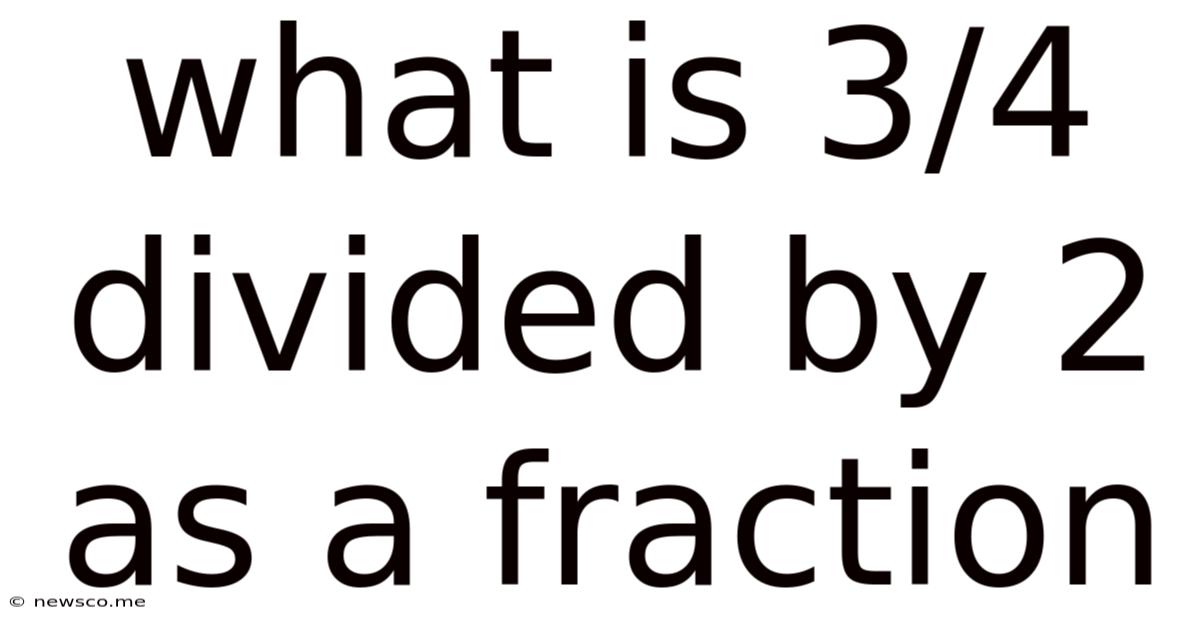
Table of Contents
What is 3/4 Divided by 2 as a Fraction? A Comprehensive Guide
Dividing fractions can seem daunting at first, but with a clear understanding of the process, it becomes straightforward. This comprehensive guide will walk you through solving the problem "What is 3/4 divided by 2 as a fraction?", explaining the steps involved and providing additional examples to solidify your understanding of fraction division. We'll explore the underlying mathematical principles and offer practical tips for tackling similar problems.
Understanding Fraction Division
Before diving into the specific problem, let's establish a foundational understanding of fraction division. The key concept is to remember that dividing by a number is the same as multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 2/3 is 3/2. The reciprocal of 5 is 1/5.
Therefore, the general rule for dividing fractions is:
- Keep the first fraction the same.
- Change the division sign to a multiplication sign.
- Flip the second fraction (find its reciprocal).
- Multiply the numerators (top numbers) together.
- Multiply the denominators (bottom numbers) together.
- Simplify the resulting fraction if possible.
Solving 3/4 Divided by 2
Now, let's apply this rule to our specific problem: 3/4 divided by 2.
-
Keep: We keep the first fraction, 3/4, as it is.
-
Change: We change the division sign (÷) to a multiplication sign (×).
-
Flip: We find the reciprocal of 2. Remember that 2 can be written as 2/1. Its reciprocal is 1/2.
-
Multiply: Now we multiply the fractions: (3/4) × (1/2)
- Multiply the numerators: 3 × 1 = 3
- Multiply the denominators: 4 × 2 = 8
-
Result: Our initial result is 3/8.
-
Simplify: In this case, the fraction 3/8 is already in its simplest form. There are no common factors between 3 and 8 other than 1.
Therefore, 3/4 divided by 2 is 3/8.
Visualizing the Problem
It can be helpful to visualize fraction division. Imagine you have a pizza cut into four equal slices. You have three of those slices (3/4 of the pizza). If you want to divide your three slices equally between two people, each person would get 3/8 of the original pizza. This visual representation reinforces the mathematical result.
Further Examples of Fraction Division
Let's work through a few more examples to reinforce the concept of fraction division:
Example 1: 1/2 divided by 1/4
- Keep: 1/2
- Change: ×
- Flip: 4/1
- Multiply: (1/2) × (4/1) = 4/2
- Simplify: 4/2 = 2
Therefore, 1/2 divided by 1/4 is 2.
Example 2: 5/6 divided by 3
- Keep: 5/6
- Change: ×
- Flip: 1/3
- Multiply: (5/6) × (1/3) = 5/18
- Simplify: 5/18 is already in its simplest form.
Therefore, 5/6 divided by 3 is 5/18.
Example 3: 2 1/3 divided by 1/2
This example introduces a mixed number (2 1/3). First, convert the mixed number into an improper fraction:
2 1/3 = (2 × 3 + 1) / 3 = 7/3
Now, proceed with the division:
- Keep: 7/3
- Change: ×
- Flip: 2/1
- Multiply: (7/3) × (2/1) = 14/3
- Simplify: 14/3 can be converted back to a mixed number: 4 2/3
Therefore, 2 1/3 divided by 1/2 is 4 2/3.
Common Mistakes to Avoid
When dividing fractions, several common mistakes can lead to incorrect answers. Let's address these pitfalls:
-
Forgetting to find the reciprocal: Remember the crucial step of flipping the second fraction before multiplying. Simply multiplying the fractions as they are will produce an incorrect result.
-
Incorrectly simplifying fractions: Always ensure that your final answer is simplified to its lowest terms. Look for common factors between the numerator and the denominator to reduce the fraction.
-
Confusing division and multiplication: Keep in mind the fundamental difference between dividing and multiplying fractions. They involve distinct processes.
-
Improper fraction conversion errors: When dealing with mixed numbers, ensure accurate conversion to improper fractions before proceeding with the division.
Practical Applications of Fraction Division
Fraction division isn't just a theoretical concept; it has numerous practical applications in everyday life and various fields:
-
Cooking and Baking: Adjusting recipes, dividing ingredients, and calculating portions often involve fraction division.
-
Sewing and Crafting: Cutting fabric, measuring materials, and scaling patterns frequently require precise fraction calculations.
-
Construction and Engineering: Dividing lengths, calculating materials, and scaling blueprints necessitate fraction division.
-
Financial Calculations: Portioning payments, distributing shares, and calculating percentages often involve fractions and division.
Conclusion
Mastering fraction division is a valuable skill with widespread applicability. By understanding the process of keeping, changing, flipping, and simplifying, you can confidently tackle fraction division problems. Remember to practice regularly and avoid common mistakes to ensure accuracy. This guide provides a solid foundation for tackling more complex fraction problems and real-world applications. Through consistent practice and a clear understanding of the underlying principles, you can confidently navigate the world of fraction division. Remember to always double-check your work and utilize visualization techniques to enhance your comprehension. With continued practice, you'll find that fraction division becomes second nature.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 3/4 Divided By 2 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.