What Is 3 4 Times 8
News Co
Mar 18, 2025 · 5 min read
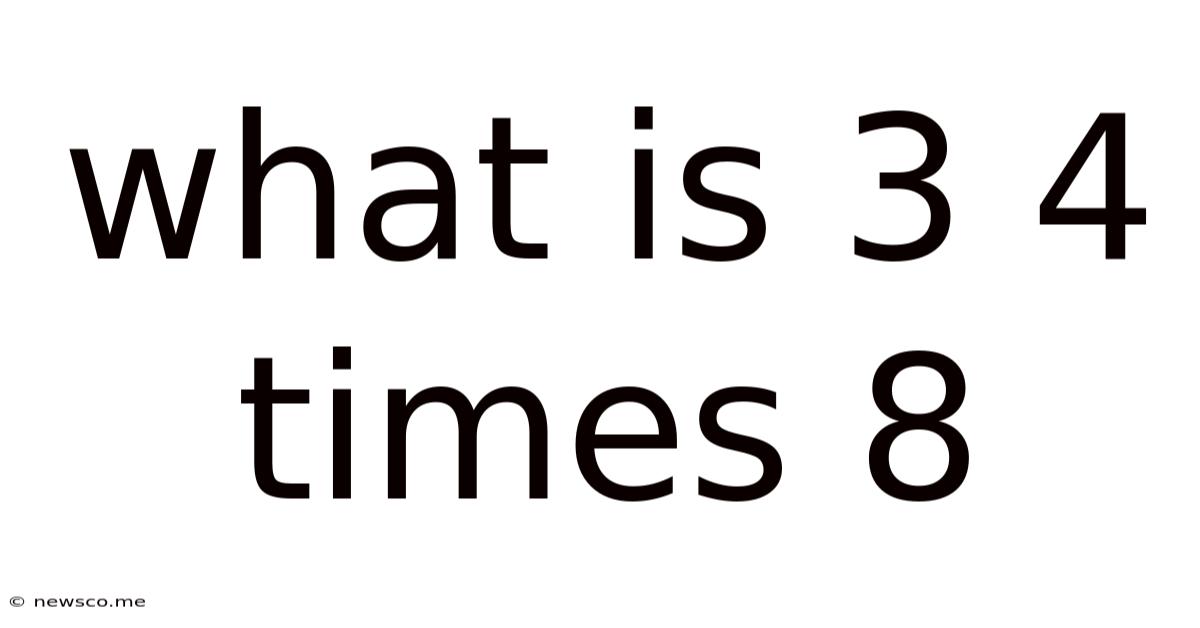
Table of Contents
What is 3/4 Times 8? A Deep Dive into Fractions and Multiplication
This seemingly simple question, "What is 3/4 times 8?", opens a door to a deeper understanding of fractions, multiplication, and the interconnectedness of mathematical concepts. While the answer itself is straightforward, exploring the various ways to solve this problem reveals fundamental principles applicable to more complex mathematical scenarios. This article will delve into different methods of calculation, explore the underlying concepts, and illustrate the practical applications of understanding fractions and multiplication.
Understanding the Problem: 3/4 x 8
Before diving into the solutions, let's break down the problem: "3/4 times 8" represents the multiplication of a fraction (3/4) and a whole number (8). This type of problem is frequently encountered in everyday life, from calculating cooking ingredients to determining discounts in shopping. Mastering this type of calculation is crucial for various mathematical and real-world applications.
The Concept of Fractions
A fraction represents a part of a whole. It consists of two parts: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. In our problem, 3/4 means we have 3 parts out of a total of 4 equal parts.
The Concept of Multiplication
Multiplication is a fundamental arithmetic operation that represents repeated addition. When we multiply 3/4 by 8, we are essentially adding 3/4 to itself eight times. Understanding this underlying principle helps visualize and conceptualize the problem.
Methods for Solving 3/4 x 8
There are several methods to solve this problem, each offering a unique perspective and reinforcing different mathematical concepts.
Method 1: Direct Multiplication
The most straightforward method involves directly multiplying the numerator of the fraction by the whole number:
3/4 x 8 = (3 x 8) / 4 = 24/4
Then, simplify the resulting fraction by dividing the numerator by the denominator:
24/4 = 6
Therefore, 3/4 times 8 equals 6.
Method 2: Converting the Whole Number to a Fraction
This method involves converting the whole number 8 into a fraction with a denominator of 1:
8 = 8/1
Now, multiply the two fractions:
3/4 x 8/1 = (3 x 8) / (4 x 1) = 24/4
Again, simplify the fraction:
24/4 = 6
This method reinforces the concept that whole numbers can be represented as fractions and highlights the consistency of the multiplication process for both fractions and whole numbers.
Method 3: Simplifying Before Multiplication
This method leverages the commutative and associative properties of multiplication to simplify the calculation before performing the multiplication. We can observe that 8 is divisible by 4:
8 = 4 x 2
Now, rewrite the problem:
3/4 x (4 x 2) = (3/4 x 4) x 2
Notice that 4/4 simplifies to 1:
(3 x 1) x 2 = 6
This method highlights the efficiency gained by simplifying before performing the full calculation, a valuable skill in more complex mathematical problems.
Method 4: Visual Representation
A visual approach can be particularly helpful for understanding the concept. Imagine a pizza cut into 4 equal slices. 3/4 of the pizza represents 3 slices. If you have 8 pizzas, each with 3 slices representing 3/4, the total number of slices would be 3 x 8 = 24 slices. Since each pizza has 4 slices, the total number of pizzas would be 24/4 = 6. This visual representation provides a concrete understanding of the problem and solution.
Expanding the Concept: Applications and Further Exploration
The simple problem "3/4 times 8" serves as a stepping stone to understanding more complex concepts.
Real-World Applications
- Cooking: If a recipe calls for 3/4 cup of sugar per serving and you're making 8 servings, you'll need 3/4 x 8 = 6 cups of sugar.
- Shopping: If an item is discounted by 3/4 of its original price and the original price is $8, the discount would be 3/4 x $8 = $6.
- Measurement: If a piece of wood is 8 meters long and you need 3/4 of it, the length you need would be 3/4 x 8 = 6 meters.
Extending to More Complex Problems
Understanding this fundamental calculation allows you to tackle more complex fraction multiplication problems. For instance, multiplying two fractions together involves multiplying the numerators and denominators separately, then simplifying the resulting fraction. Similarly, multiplying a fraction by a decimal involves converting either the fraction or the decimal to the other form before multiplication.
Understanding the Relationship Between Fractions and Decimals
Fractions and decimals are two ways of representing parts of a whole. 3/4 can be expressed as a decimal by dividing the numerator by the denominator: 3 ÷ 4 = 0.75. This conversion allows for flexibility in problem-solving, allowing you to choose the most convenient form for a particular calculation.
Importance of Simplifying Fractions
Simplifying fractions, also known as reducing fractions, is crucial for obtaining the most concise and accurate representation of a value. Simplifying fractions makes calculations easier and reduces the chance of errors.
Conclusion: Mastering Fractions and Multiplication
The seemingly simple question, "What is 3/4 times 8?", unveils a wealth of mathematical concepts and their practical applications. Understanding various methods of solving this problem, from direct multiplication to visual representations, builds a strong foundation in fraction multiplication and reinforces the interconnectedness of mathematical concepts. This foundation will prove invaluable in tackling more complex mathematical problems and in various real-world applications where the ability to calculate fractions accurately is essential. The key takeaway is not merely the answer (6), but the understanding of the underlying principles and the ability to apply these principles to a wider range of mathematical problems.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 3 4 Times 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.