What Is 3 Divided By 1/2
News Co
Apr 23, 2025 · 6 min read
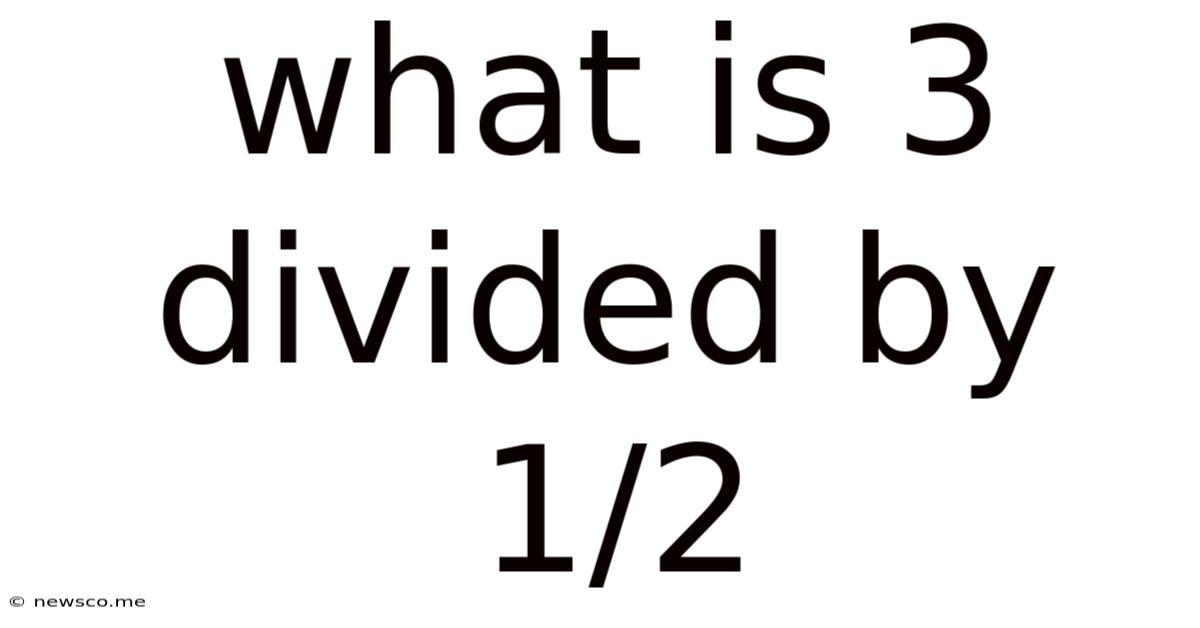
Table of Contents
What is 3 Divided by 1/2? Unpacking Fraction Division
The seemingly simple question, "What is 3 divided by 1/2?", often trips up students and adults alike. While the answer itself is straightforward (6), the underlying concept of dividing by fractions requires a deeper understanding. This article will thoroughly explore this problem, explaining the process, providing multiple approaches to solving it, and highlighting the broader implications of fraction division in mathematics.
Understanding the Problem: 3 ÷ 1/2
Before diving into the solution, let's clarify what the question "3 ÷ 1/2" actually means. It asks: "How many halves (1/2) are there in 3?" This reframing helps visualize the problem and makes the solution more intuitive. Imagine you have three whole pizzas, and you want to divide each pizza into halves. How many half-pizzas would you have? This visual representation immediately suggests the answer is 6.
Method 1: The "Keep, Change, Flip" Method (Reciprocal Method)
This is arguably the most common and efficient method for dividing fractions. It's based on the principle that dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down.
Steps:
- Keep: Keep the first number (dividend) the same: 3
- Change: Change the division sign (÷) to a multiplication sign (×): 3 ×
- Flip: Flip the second number (divisor) – find its reciprocal: 1/2 becomes 2/1 (or simply 2)
- Multiply: Multiply the numbers: 3 × 2 = 6
Therefore, 3 ÷ 1/2 = 6.
This method is highly efficient and works reliably for all fraction division problems. Its simplicity makes it a favorite among students and teachers. However, understanding why this method works is crucial for a truly comprehensive understanding.
Method 2: Visual Representation with Fraction Models
A visual approach is incredibly helpful, especially for those who struggle with abstract mathematical concepts. We can represent this problem using circles or other shapes to visualize the fractions.
Imagine three whole circles representing the number 3. Now, divide each circle in half. You'll end up with six half-circles. This visual demonstration clearly shows that there are six halves in three wholes. This method solidifies the understanding of the concept rather than just memorizing a process. Using visual aids like this is especially effective for younger learners.
Method 3: Converting to Improper Fractions
Another approach involves converting the whole number into a fraction and then applying the standard fraction division rule.
Steps:
- Convert to Fractions: Rewrite 3 as 3/1. The problem becomes (3/1) ÷ (1/2).
- Keep, Change, Flip: Apply the "Keep, Change, Flip" method: (3/1) × (2/1)
- Multiply: Multiply the numerators and denominators: (3 × 2) / (1 × 1) = 6/1 = 6
This method reinforces the understanding of fractions and their manipulation, highlighting the equivalence of whole numbers and fractions. It builds on the foundational understanding of fractional representation.
Method 4: Using the Definition of Division
Division, at its core, is about finding how many times one number (the divisor) goes into another number (the dividend). In the case of 3 ÷ 1/2, we're asking how many times 1/2 goes into 3.
We can repeatedly subtract 1/2 from 3 until we reach zero. Let's illustrate:
3 - 1/2 = 2 1/2 2 1/2 - 1/2 = 2 2 - 1/2 = 1 1/2 1 1/2 - 1/2 = 1 1 - 1/2 = 1/2 1/2 - 1/2 = 0
We subtracted 1/2 six times to reach zero. This demonstrates that there are six halves in three wholes. This method explicitly connects division to its foundational definition, enhancing conceptual understanding.
Why the "Keep, Change, Flip" Method Works
The success of the "Keep, Change, Flip" method is rooted in the mathematical properties of reciprocals and multiplication. Dividing by a fraction is equivalent to multiplying by its reciprocal because:
- Division is the inverse of multiplication: If a × b = c, then c ÷ b = a.
- Reciprocals multiply to 1: Any number multiplied by its reciprocal equals 1. (e.g., (1/2) × (2/1) = 1)
Let's analyze 3 ÷ (1/2):
We can rewrite this as a complex fraction: 3 / (1/2). To simplify this, we multiply both the numerator and the denominator by the reciprocal of the denominator (2/1):
(3 × (2/1)) / ((1/2) × (2/1)) = (6/1) / 1 = 6
This shows that the "Keep, Change, Flip" method is not just a shortcut but a mathematically sound procedure derived from fundamental algebraic principles.
Real-World Applications of Fraction Division
Fraction division isn't just an abstract mathematical concept; it has numerous practical applications in everyday life and various professions:
- Cooking: Recipes often require dividing ingredients into fractions. For example, if a recipe calls for 1/2 cup of flour per serving and you want to make 3 servings, you'd need to calculate 3 ÷ (1/2) to determine the total amount of flour needed.
- Construction and Engineering: Many construction and engineering projects involve precise measurements and calculations using fractions. Dividing materials or distances accurately is crucial for successful projects.
- Sewing and Tailoring: Cutting fabric for clothing requires precise measurements involving fractions. Determining the amount of fabric needed based on pattern instructions frequently involves fraction division.
- Data Analysis: In data analysis, dealing with proportions and ratios commonly involves working with fractions and division.
Common Mistakes and How to Avoid Them
Several common mistakes can occur when dealing with fraction division:
- Forgetting to flip the fraction: Students may forget to take the reciprocal of the second fraction, leading to an incorrect answer. Careful attention to each step of the "Keep, Change, Flip" method is essential.
- Incorrectly multiplying fractions: Errors can arise in multiplying the numerators and denominators. Double-checking multiplication is crucial.
- Not understanding the concept: Memorizing the procedure without understanding the underlying principles can lead to confusion and mistakes. A firm grasp of the concepts is paramount for success.
Mastering Fraction Division: Practice and Resources
Consistent practice is key to mastering fraction division. Working through various examples, both simple and complex, will build confidence and proficiency. Many online resources, including educational websites and apps, provide practice problems and interactive exercises.
Start with simple problems like the one discussed in this article (3 ÷ 1/2) and gradually progress to more challenging examples involving mixed numbers and larger fractions. Remember, understanding the concept is just as important as the procedural steps.
Conclusion: Beyond the Answer of 6
While the answer to "What is 3 divided by 1/2?" is unequivocally 6, the true value of this problem lies in the deeper understanding it unlocks about fraction division. By exploring different methods and delving into the underlying mathematical principles, we gain a comprehensive understanding not only of how to solve this particular problem but also how to confidently approach all future fraction division challenges. Mastering this seemingly simple concept opens doors to more advanced mathematical concepts and real-world applications. The ability to confidently and accurately work with fractions is a valuable skill across a range of disciplines.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 3 Divided By 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.