What Is 3 Out Of 5 As A Percentage
News Co
Apr 05, 2025 · 5 min read
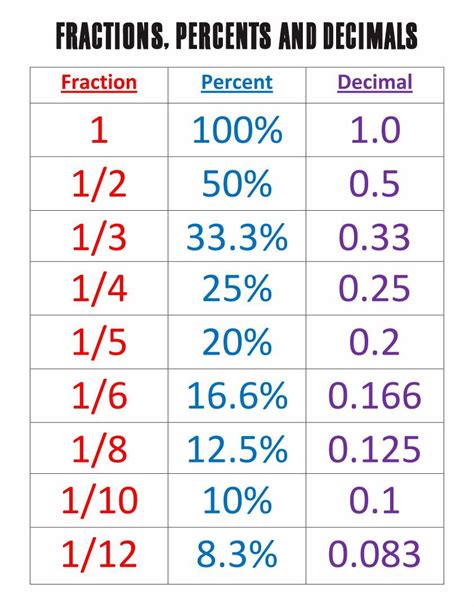
Table of Contents
What is 3 out of 5 as a Percentage? A Comprehensive Guide
Knowing how to convert fractions to percentages is a fundamental skill with wide-ranging applications in everyday life, from calculating discounts and tips to understanding statistics and data analysis. This article dives deep into the seemingly simple question: What is 3 out of 5 as a percentage? We'll not only provide the answer but also explore the underlying principles, different methods of calculation, and practical examples to solidify your understanding.
Understanding Fractions and Percentages
Before we tackle the core question, let's establish a clear understanding of fractions and percentages.
Fractions: A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). In our case, "3 out of 5" is represented as the fraction 3/5. The numerator (3) indicates the number of parts we're interested in, while the denominator (5) represents the total number of parts.
Percentages: A percentage is simply a fraction expressed as a proportion of 100. The symbol "%" represents "per cent" or "out of 100." So, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Calculating 3 out of 5 as a Percentage: Three Methods
There are several ways to calculate 3 out of 5 as a percentage. Let's explore three common methods:
Method 1: Direct Conversion using Division
This is arguably the most straightforward method. We convert the fraction 3/5 into a decimal, then multiply by 100 to express it as a percentage.
- Divide the numerator by the denominator: 3 ÷ 5 = 0.6
- Multiply the result by 100: 0.6 × 100 = 60
- Add the percentage symbol: 60%
Therefore, 3 out of 5 is 60%.
Method 2: Creating an Equivalent Fraction with a Denominator of 100
This method involves finding an equivalent fraction where the denominator is 100. This directly gives us the percentage.
- Find the multiplier to reach 100: To get from 5 to 100, we multiply by 20 (100 ÷ 5 = 20).
- Multiply both the numerator and denominator by this multiplier: (3 × 20) / (5 × 20) = 60/100
- Express as a percentage: 60/100 = 60%
Again, we arrive at the answer: 3 out of 5 is 60%.
Method 3: Using Proportions
This method uses the concept of proportions to solve for the unknown percentage.
We set up a proportion:
3/5 = x/100
Where 'x' represents the unknown percentage.
To solve for x, we cross-multiply:
5x = 300
Then divide both sides by 5:
x = 60
Therefore, 3 out of 5 is 60%.
Practical Applications of Percentage Calculations
Understanding how to convert fractions to percentages has numerous practical applications in various aspects of life:
1. Retail Discounts and Sales:
Imagine a store offering a 20% discount on an item. If the original price is $100, the discount amount is 20% of $100, which is $20. Similar calculations are used for sales tax, interest rates, and more.
2. Grade Calculation:
If you answer 3 out of 5 questions correctly on a quiz, your score is 60%. This is a common method for determining grades in educational settings.
3. Statistical Analysis:
Percentages are fundamental in statistical analysis. Understanding percentages allows you to interpret data represented in charts and graphs, make informed decisions, and draw accurate conclusions. For example, understanding market share percentages or survey results often requires converting fractions to percentages.
4. Financial Calculations:
Percentage calculations are essential for understanding financial statements, calculating interest on loans and investments, evaluating investment returns, and understanding profit margins.
5. Everyday Life:
Beyond formal settings, percentage calculations are used to calculate tips at restaurants, determine the percentage of a task completed, and even understand weather forecasts (e.g., a 60% chance of rain).
Beyond the Basics: Working with More Complex Fractions
The principles discussed above can be applied to more complex fractions. For instance, let's consider the fraction 17/25. We can use the same methods to convert it to a percentage:
Method 1 (Division): 17 ÷ 25 = 0.68; 0.68 × 100 = 68%
Method 2 (Equivalent Fraction): To get from 25 to 100, we multiply by 4. (17 × 4) / (25 × 4) = 68/100 = 68%
Method 3 (Proportion): 17/25 = x/100; 25x = 1700; x = 68%
Thus, 17/25 is equivalent to 68%.
Troubleshooting Common Errors
While the process of converting fractions to percentages is relatively straightforward, some common errors can occur:
-
Incorrect Division: Ensuring accuracy in the initial division step is critical. Double-check your calculations to avoid errors that can significantly impact the final percentage.
-
Forgetting to Multiply by 100: Remember that the decimal result of the division needs to be multiplied by 100 to express it as a percentage.
-
Incorrect Interpretation of the Fraction: Make sure you correctly identify the numerator and the denominator in the fraction before proceeding with the calculation.
Conclusion
Converting fractions to percentages is a crucial skill for navigating various aspects of life. The question, "What is 3 out of 5 as a percentage?" serves as a simple yet effective illustration of this fundamental concept. By mastering the methods outlined in this article, you'll be well-equipped to handle a wide range of percentage calculations with confidence and accuracy. Whether it's understanding discounts, analyzing data, or making informed financial decisions, the ability to convert fractions to percentages empowers you to make sense of the numerical world around you. Remember to practice regularly to solidify your understanding and build fluency in these essential mathematical skills. The more you practice, the easier and faster these conversions will become.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 3 Out Of 5 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.