What Is 3 To The 3 Power
News Co
Apr 08, 2025 · 5 min read
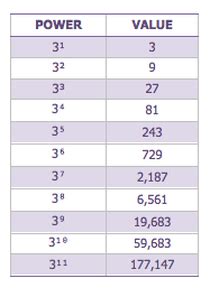
Table of Contents
What is 3 to the 3rd Power? A Deep Dive into Exponents and Their Applications
Understanding exponents is fundamental to mathematics and numerous scientific fields. This article delves into the concept of "3 to the 3rd power," explaining its meaning, calculation, practical applications, and related mathematical concepts. We'll explore this seemingly simple calculation in detail, unveiling its significance within a broader mathematical context.
Understanding Exponents: The Basics
Before we tackle 3 to the 3rd power (also written as 3³), let's establish a solid foundation in exponents. An exponent, or power, indicates how many times a base number is multiplied by itself. It's represented as a small superscript number to the right of the base.
For example, in the expression xⁿ, 'x' is the base, and 'n' is the exponent. This signifies that 'x' is multiplied by itself 'n' times.
Examples:
- 2² = 2 x 2 = 4 (2 to the power of 2, or 2 squared)
- 5³ = 5 x 5 x 5 = 125 (5 to the power of 3, or 5 cubed)
- 10⁴ = 10 x 10 x 10 x 10 = 10,000 (10 to the power of 4, or 10 raised to the fourth power)
Calculating 3 to the 3rd Power (3³)
Now, let's focus on our specific question: What is 3 to the 3rd power? This means we need to multiply the base number 3 by itself three times:
3³ = 3 x 3 x 3 = 27
Therefore, 3 to the 3rd power is equal to 27. This simple calculation forms the basis for understanding more complex exponential equations and their applications across various disciplines.
Expanding on Exponents: Rules and Properties
Understanding the basic calculation is only the beginning. Several crucial rules govern how exponents behave, enabling us to simplify and solve more complex expressions.
1. Product of Powers Rule:
When multiplying two numbers with the same base, you add their exponents: xᵃ * xᵇ = x⁽ᵃ⁺ᵇ⁾
Example: 2² * 2³ = 2⁽²⁺³⁾ = 2⁵ = 32
2. Quotient of Powers Rule:
When dividing two numbers with the same base, you subtract their exponents: xᵃ / xᵇ = x⁽ᵃ⁻ᵇ⁾ (where x ≠ 0)
Example: 5⁵ / 5² = 5⁽⁵⁻²⁾ = 5³ = 125
3. Power of a Power Rule:
When raising a power to another power, you multiply the exponents: (xᵃ)ᵇ = x⁽ᵃ*ᵇ⁾
Example: (4²)³ = 4⁽²*³⁾ = 4⁶ = 4096
4. Power of a Product Rule:
When raising a product to a power, you raise each factor to that power: (xy)ⁿ = xⁿyⁿ
Example: (2*3)² = 2² * 3² = 4 * 9 = 36
5. Power of a Quotient Rule:
When raising a quotient to a power, you raise both the numerator and the denominator to that power: (x/y)ⁿ = xⁿ/yⁿ (where y ≠ 0)
Example: (4/2)² = 4²/2² = 16/4 = 4
Applications of Exponents in Real-World Scenarios
Exponents are not confined to theoretical mathematics; they have extensive practical applications in various fields:
1. Compound Interest:
Calculating compound interest relies heavily on exponents. The formula A = P(1 + r/n)^(nt) uses exponents to determine the future value (A) of an investment based on the principal amount (P), interest rate (r), number of times interest is compounded per year (n), and the number of years (t). Understanding exponents is crucial for anyone managing investments or loans.
2. Population Growth:
Exponential growth models are frequently used to predict population increases (whether it's human populations, animal populations, or bacterial colonies). The formula often involves an exponent to represent the rate of growth over time.
3. Radioactive Decay:
Radioactive decay, a process where unstable atomic nuclei lose energy by emitting radiation, follows an exponential decay model. Exponents are instrumental in determining the remaining amount of a radioactive substance after a certain period. This is crucial in fields like nuclear physics, medicine (radioactive dating), and environmental science.
4. Computer Science:
Exponents are fundamental in computer science, particularly in algorithms and data structures. Analyzing algorithm efficiency often involves expressing time complexity using exponential notation (e.g., O(2ⁿ)). Understanding exponents is vital for optimizing algorithms and improving software performance.
5. Physics and Engineering:
Many physical phenomena, such as wave propagation, light intensity, and electrical circuits, can be modeled using exponential functions. Engineers and physicists use exponential equations to design systems and analyze their behavior.
6. Finance:
Beyond compound interest, exponents play a role in options pricing models (like the Black-Scholes model), which are essential tools in financial markets. These models use exponential functions to calculate the theoretical value of options contracts.
7. Biology:
Exponential growth and decay are also fundamental concepts in various biological processes, such as cell division and the spread of diseases. Understanding exponential functions is crucial for modeling these processes and predicting their outcomes.
Beyond 3 to the 3rd Power: Exploring Higher Exponents
While we've focused on 3³, understanding exponents extends to much larger numbers. Consider the following examples:
- 3⁴ = 3 x 3 x 3 x 3 = 81
- 3⁵ = 3 x 3 x 3 x 3 x 3 = 243
- 3¹⁰ = 59,049
As you can see, the values increase rapidly as the exponent grows. This rapid increase is characteristic of exponential functions and is a key reason why they are so important in modeling various real-world phenomena involving growth or decay.
Scientific Notation and Exponents
For extremely large or small numbers, scientific notation is used. This notation employs exponents to express numbers concisely. A number is written in the form a x 10ⁿ, where 'a' is a number between 1 and 10, and 'n' is an integer exponent.
Example: The speed of light is approximately 300,000,000 meters per second. In scientific notation, this is written as 3 x 10⁸ m/s.
Conclusion: The Significance of Understanding 3 to the 3rd Power and Beyond
While the calculation of 3 to the 3rd power (3³ = 27) might seem simple at first glance, it serves as a gateway to a vast and crucial area of mathematics—the world of exponents. From understanding compound interest to modeling population growth and radioactive decay, the principles of exponents are applied across multiple disciplines. Mastering these principles is essential for anyone seeking a deeper understanding of mathematics and its applications in the real world. The seemingly simple calculation of 3³ unleashes a powerful tool for solving complex problems and understanding the intricacies of the universe around us.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 3 To The 3 Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.