What Is 3 To The Power Of 3
News Co
Mar 15, 2025 · 5 min read
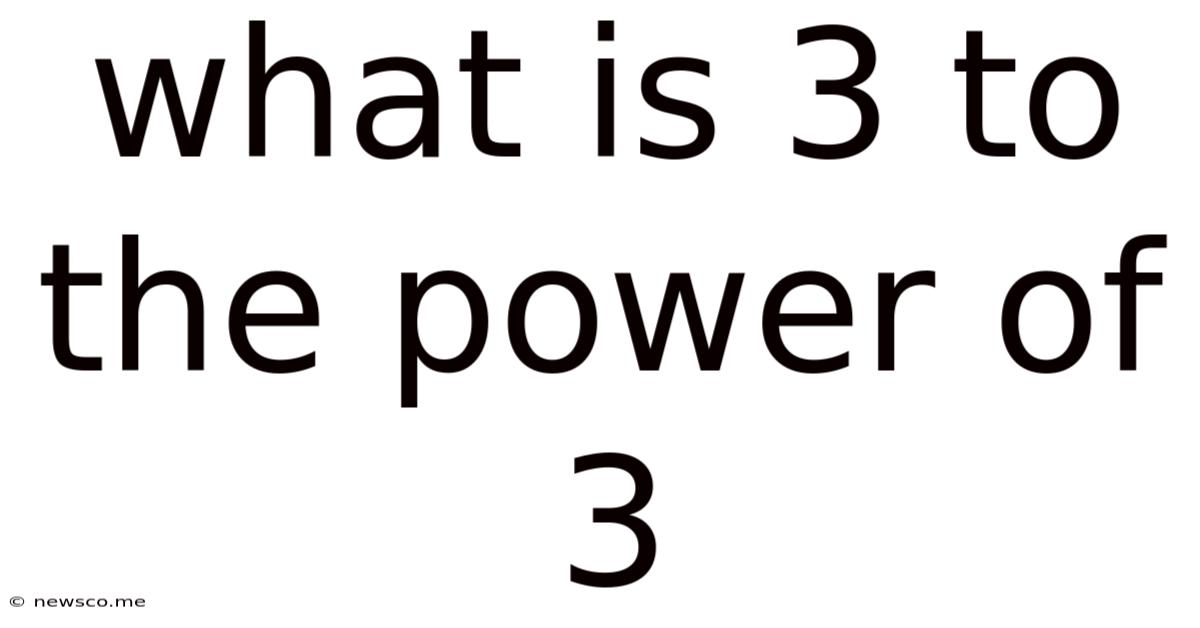
Table of Contents
What is 3 to the Power of 3? A Deep Dive into Exponents and Their Applications
The seemingly simple question, "What is 3 to the power of 3?" opens a door to a vast world of mathematical concepts, practical applications, and intriguing historical context. This seemingly elementary calculation – 3³ – is far more significant than it initially appears, serving as a foundational element in various fields, from basic arithmetic to advanced calculus and computer science. Let's explore this concept in detail.
Understanding Exponents: The Fundamentals
Before delving into the specifics of 3³, it's crucial to grasp the fundamental concept of exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. The general form is written as b<sup>n</sup>, where 'b' represents the base and 'n' represents the exponent. In this notation, b<sup>n</sup> means 'b multiplied by itself n times'.
For instance:
- 2<sup>2</sup> = 2 x 2 = 4 (2 squared or 2 to the power of 2)
- 2<sup>3</sup> = 2 x 2 x 2 = 8 (2 cubed or 2 to the power of 3)
- 2<sup>4</sup> = 2 x 2 x 2 x 2 = 16 (2 to the power of 4)
Therefore, 3 to the power of 3, denoted as 3³, signifies 3 multiplied by itself three times:
3³ = 3 x 3 x 3 = 27
This simple calculation, yielding the answer 27, serves as the foundation for more complex mathematical operations and applications.
Beyond the Basic Calculation: Exploring the Significance of 3³
While the calculation itself is straightforward, understanding the broader implications of 3³ reveals its importance across numerous disciplines:
1. Geometric Applications: Volume and Cubes
The expression 3³ has a direct geometric interpretation. Imagine a cube, a three-dimensional shape with equal sides. If each side of the cube measures 3 units (e.g., centimeters, inches), then 3³ represents the volume of that cube. This is because the volume of a cube is calculated by multiplying the length, width, and height, all of which are equal in a cube. Therefore, a cube with 3-unit sides has a volume of 3 x 3 x 3 = 27 cubic units. This concept extends to other three-dimensional shapes and their volume calculations.
2. Algebraic Manipulations: Equations and Polynomials
The number 27, derived from 3³, frequently appears in algebraic equations and polynomial expressions. Understanding exponents is crucial for simplifying, solving, and manipulating these expressions. For example, consider the equation: x³ = 27. Solving for 'x' requires recognizing that x = 3 is the solution, as 3³ = 27. This simple example demonstrates how the concept of 3³ underpins more complex algebraic problems.
3. Computer Science and Binary Systems: Data Representation
In computer science, binary systems (base-2) are fundamental. While not directly related to 3³, understanding exponential notation is essential for comprehending how computers represent and manipulate data. Large data sets are often described using powers of 2 (e.g., kilobytes, megabytes, gigabytes), which are fundamentally based on the same exponential principles as 3³. The ability to grasp and work with exponents is crucial for understanding data structures and algorithms.
4. Scientific Notation: Expressing Large and Small Numbers
Scientific notation utilizes exponents to represent extremely large or small numbers concisely. For instance, the speed of light is approximately 3 x 10<sup>8</sup> meters per second. This notation is far more manageable than writing out the full number (300,000,000). The principles behind scientific notation rely heavily on the understanding of exponents and their ability to efficiently convey magnitude.
5. Compound Interest Calculations: Financial Applications
Exponential growth is a key concept in finance, especially when dealing with compound interest. The formula for compound interest involves exponents to calculate the future value of an investment. Understanding exponents allows for accurate predictions of investment growth over time. This is a crucial component in personal finance, business planning, and economic forecasting.
Expanding the Concept: Exponents Beyond 3³
While we've focused on 3³, the principles of exponents extend far beyond this single example. Understanding exponents allows us to tackle a wide range of mathematical problems:
- Negative Exponents: b<sup>-n</sup> = 1/b<sup>n</sup>. This means a negative exponent indicates the reciprocal of the positive exponent.
- Fractional Exponents: b<sup>m/n</sup> represents the nth root of b raised to the power of m. For example, 4<sup>1/2</sup> = √4 = 2.
- Zero Exponent: b<sup>0</sup> = 1. Any non-zero number raised to the power of zero is always 1.
Mastering these extended concepts enhances problem-solving capabilities in numerous mathematical fields.
Real-World Applications: Beyond the Classroom
The application of exponential concepts, including 3³, extends far beyond theoretical mathematics. Here are a few examples illustrating its real-world relevance:
- Population Growth: Modeling population growth often involves exponential functions, reflecting the multiplicative nature of reproduction.
- Radioactive Decay: The decay of radioactive materials follows an exponential pattern, with the amount of material decreasing exponentially over time.
- Spread of Diseases: Epidemiological models often use exponential functions to predict the spread of infectious diseases.
- Computer Algorithms: Many algorithms in computer science utilize exponential concepts for efficiency and complexity analysis.
Historical Context: The Evolution of Exponential Notation
The concept of exponents has evolved over centuries, with mathematicians refining notation and understanding. Early forms of exponential notation were less standardized, making calculations more cumbersome. The current notation, with the base and exponent clearly defined, has significantly simplified mathematical operations and communication. Understanding this historical context provides a richer appreciation for the mathematical tools we use today.
Conclusion: The Enduring Power of 3³
The seemingly simple calculation of 3³ – yielding the result 27 – is much more than a basic arithmetic problem. It serves as a fundamental building block for various mathematical and scientific fields, representing a core concept that underpins a wide range of real-world applications. From calculating the volume of a cube to understanding exponential growth in finance, the principles of exponents, as exemplified by 3³, are essential for anyone seeking to comprehend the world around them through a mathematical lens. Understanding 3³ is not just about the answer; it's about understanding the underlying power of exponential notation and its pervasive influence across various disciplines. The significance of this seemingly simple calculation extends far beyond its immediate result, revealing its importance as a cornerstone of mathematical understanding and problem-solving.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 3 To The Power Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.