What Is 3 To The Power Of 6
News Co
Apr 05, 2025 · 4 min read
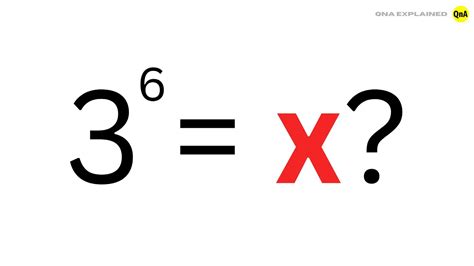
Table of Contents
- What Is 3 To The Power Of 6
- Table of Contents
- What is 3 to the Power of 6? A Deep Dive into Exponentiation
- Understanding Exponents
- Calculating 3 to the Power of 6
- Applications of Exponents and Exponential Growth
- 1. Finance and Investing:
- 2. Science and Technology:
- 3. Computer Science:
- 4. Biology:
- 5. Physics:
- Beyond 3 to the Power of 6: Exploring Larger Exponents
- Conclusion: The Significance of Exponents
- Latest Posts
- Related Post
What is 3 to the Power of 6? A Deep Dive into Exponentiation
The seemingly simple question, "What is 3 to the power of 6?" opens a door to a fascinating world of mathematics, specifically exponentiation. While the answer itself is straightforward – 729 – the journey to understanding how we arrive at this answer, and the broader implications of exponential growth, reveals much more. This article will explore not only the calculation of 3<sup>6</sup> but also delve into the concepts of exponents, their applications, and their significance in various fields.
Understanding Exponents
Before we tackle 3<sup>6</sup>, let's establish a firm grasp of what exponents, or powers, represent. An exponent indicates how many times a base number is multiplied by itself. In the expression a<sup>b</sup>, a is the base and b is the exponent. So, 3<sup>6</sup> means 3 multiplied by itself 6 times: 3 × 3 × 3 × 3 × 3 × 3.
This seemingly simple concept has far-reaching consequences. Exponential growth, characterized by an exponent, is vastly different from linear growth. Linear growth increases at a constant rate, while exponential growth increases at an increasing rate. This difference becomes dramatically apparent as the exponent increases.
Calculating 3 to the Power of 6
Now, let's calculate 3<sup>6</sup>:
3 × 3 = 9 9 × 3 = 27 27 × 3 = 81 81 × 3 = 243 243 × 3 = 729
Therefore, 3<sup>6</sup> = 729.
This might seem trivial for small numbers, but the magnitude of exponential growth quickly becomes impressive as the base and exponent increase. Consider 3<sup>10</sup>, which would be 59,049, a considerably larger number. This demonstrates the power of exponential growth.
Applications of Exponents and Exponential Growth
Exponents are not just abstract mathematical concepts; they have practical applications across numerous fields:
1. Finance and Investing:
Compound interest is a prime example of exponential growth. When interest is calculated not only on the principal amount but also on accumulated interest, the growth accelerates exponentially. Understanding exponential growth is crucial for comprehending investment strategies, loan repayments, and financial planning. A small initial investment can grow substantially over time due to the exponential nature of compound interest.
2. Science and Technology:
Exponential growth is prevalent in various scientific phenomena. Population growth, radioactive decay, and the spread of viruses often follow exponential patterns. Scientists use exponential functions to model these processes and make predictions. Understanding these models is crucial for managing resources, controlling diseases, and predicting future trends.
3. Computer Science:
In computer science, the concept of Big O notation uses exponents to describe the efficiency of algorithms. The time or space complexity of an algorithm is often expressed as O(n<sup>k</sup>), where 'n' represents the input size and 'k' is an exponent. This helps computer scientists assess how the performance of an algorithm scales with increasing input size.
4. Biology:
Exponential growth is evident in biological systems. Bacterial colonies, for example, can exhibit exponential growth under ideal conditions. This concept is essential in microbiology, ecology, and medicine. The rapid reproduction rate of bacteria makes understanding exponential growth vital for managing bacterial infections and studying population dynamics.
5. Physics:
Exponents play a significant role in various physical phenomena. For instance, Newton's law of universal gravitation involves inverse-square law (proportional to 1/r<sup>2</sup>), where 'r' is the distance between two objects. The intensity of light decreases with the square of the distance from the source, another example of an inverse-square law.
Beyond 3 to the Power of 6: Exploring Larger Exponents
While we've focused on 3<sup>6</sup>, the principles of exponentiation extend to much larger exponents. Calculating these numbers manually becomes impractical, which is where calculators and computers become indispensable tools.
Understanding how to work with larger exponents involves grasping the concepts of scientific notation and logarithms. Scientific notation helps express extremely large or small numbers concisely, while logarithms provide a way to solve equations involving exponents.
For example, calculating 3<sup>100</sup> would yield an astronomical number. Scientific notation would provide a more manageable representation. Similarly, solving equations like 3<sup>x</sup> = 1000 would necessitate the use of logarithms.
Conclusion: The Significance of Exponents
The seemingly simple calculation of 3<sup>6</sup> serves as a gateway to understanding the broader implications of exponents and exponential growth. This fundamental mathematical concept finds applications in diverse fields, impacting our understanding of finance, science, technology, biology, and physics. From compound interest to the spread of diseases, the power of exponential growth is undeniable, and appreciating its nuances is crucial for navigating the complexities of the modern world. The seemingly straightforward answer, 729, represents much more than just a numerical result; it represents the beginning of a deeper understanding of a fundamental concept that shapes our world. Further exploration of logarithms, scientific notation, and more complex exponential functions will reveal even more profound insights into this powerful mathematical tool.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 3 To The Power Of 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.